Moments
F
d
In addition to the size of a force and its direction of
c
action, the location of the force is important. For
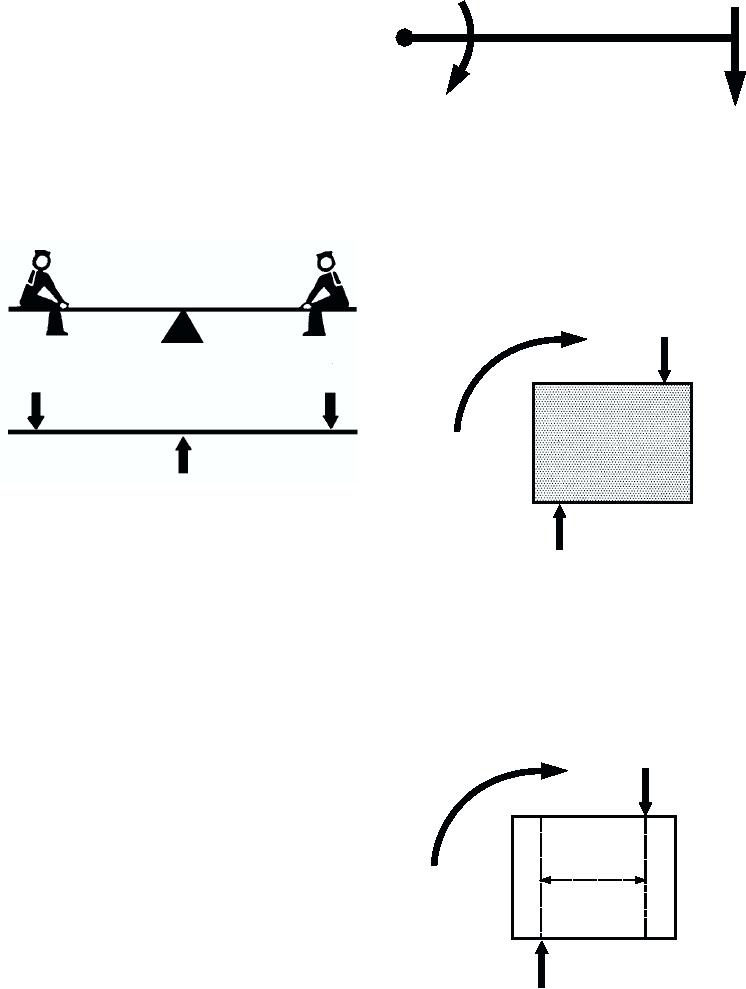
example, if two persons of the same weight sit on
opposite ends of a seesaw, equally distant from the
support (fig. 12-5), the seesaw will balance. However,
DCf1206
if one person moves, the seesaw will no longer remain
Figure 12-6. Diagram to illustrate the moment of force.
balanced. The person farthest away from the support
will move down because the effect of the force of
his/her weight is greater.
A special case of moments occurs when two equal
and opposite forces not in the same line rotate a body.
This system of two forces, as shown in figure 12-7, is
termed a COUPLE. The moment of the couple is the
product of one of the forces times the distance between
them (fig. 12-8).
DCf1205
Figure 12-5. The balanced seesaw.
DCf1207
Figure 12-7. Equal and opposite forces acting on a body (not
The effect of the location of a force is known as the
in the same line).
MOMENT OF FORCE. It is equal to the force
multiplied by the distance from an axis about which
Calculation of the moment of the couple, as shown
you want to find its effect. The moment of a force is the
in figure 12-8, is as follows:
tendency of the force to produce rotation or to move the
The moment of the couple = F x d
object around an axis. Since the force is expressed in
terms of weight units, such as tons or pounds, and the
Therefore, the moment of the couple is 50 feet
moment is force times distance, the units for moment
times 12 pounds that equals 600 foot-pounds.
are expressed as foot-tons, foot-pounds, or
inch-ounces.
F = 50 LBS.
In figure 12-6 the moment of force (F) about the
axis at point a is F times d; d being called the moment
arm. The moment of a force can be measured about any
point or axis; however, the moment differs according to
12 FT
the length of the moment arm. It should be noted that
the moment of a force tends to produce rotary motion.
In figure 12-6, for example, the force F produces a
clockwise rotation. If, at the same time, an equal and
F = 50 LBS.
opposite force produces a counterclockwise rotation,
DCf1208
there will be no rotation; and the body is in
Figure 12-8. Diagram to show calculation of the moment of a
couple.
12-4