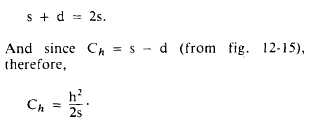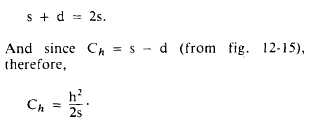tensions for tapes supported at only the ends as
follows:
For 100-ft tapes, from 20 to 30 lb
angle, A, or the difference in elevation h between
the taped stations.
When the vertical angle is used, the formula
for slope correction is as follows:
For 150-ft tapes, from 25 to 30 lb
For 200-ft tapes, from 30 to 40 lb
Generally, for a heavy 100-ft tape weighing
about 3 lb that was standardized, whether
supported throughout or at the ends only, the
systematic error per tape length caused by sag is
as follows:
10-lb tension = 0.37 ft
20-lb tension = 0.09 ft
30-lb tension = 0.04 ft
For the Engineering Aid’s survey work,
measurements are normally in the lower order of
precision. The correction for sag varies with the
cube of the unsupported length; for short spans,
it is often negligible.
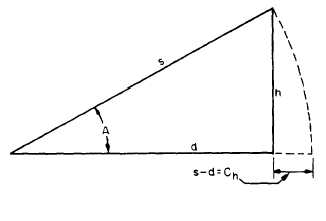
CORRECTING FOR SLOPE.— When you
take a measurement with a tape along an inclined
plane (along the natural slope of the ground),
obviously, the taped distance is greater than the
horizontal distance. This taped distance is
represented by s in figure 12-15.
The difference between the slope distance and
the horizontal distance (s – d) is called the slope
correction. This correction is always subtracted
from the slope distance. To compute for the slope
correction, you should know either the vertical
Figure 12-15.-Correction for slope distance.
When the difference in elevation is used, the
approximate formula derived by Pythagorean
theorem of a right triangle (fig. 12-15) for the
slope correction is as follows:
But for a small slope, d is approximately equal
to s; therefore,
For slopes greater than 5 percent, a closer
approximation of Ch can be determined by
expanding the above formula to this form.
12-18