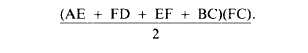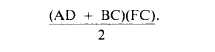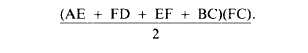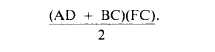The length of AB is called the base (b), and the
length of DC, the altitude (h); therefore, your for-
mula for determining the area of an oblique
triangle is again A = 1/2bh.
You must remember that in a right triangle
h corresponds to the length of one of the sides,
while in an oblique triangle it does not. Therefore,
for a right triangle with the length of the sides
given, you can determine the area by the formula
A = 1/2bh. For an oblique triangle with the
length of the sides given, you cannot use this
formula unless you can determine the value of h,
Later in this chapter you will learn trigonometric
methods of determining areas of various forms
of triangles on the basis of the length of the sides
alone.
Area of a Rhombus or Rhomboid
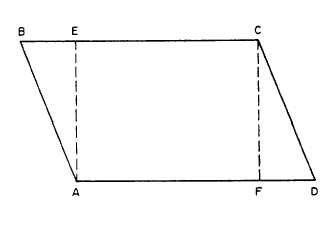
Figure 1-9 shows a rhomboid, ABCD. If you
drop a perpendicular, CF, from L C to AD, and
project another from LA to BC, you will create
two right triangles, AAEB and ACFD, and the
rectangle AECF. It can be shown geometrically
that the right triangles are similar and equal.
You can see that the area of the rectangle
AECF equals the product of AF x FC. The area
of the triangle CFD equals 1 /2(FD)(FC). Because
the triangle AEB is equal and similar to CFD, the
area of that triangle also equals 1/2(FD)(FC).
Therefore, the total area of both triangles equals
(FD)(FC). The total area of the rhomboid equals
the area of the rectangle AECF + the total area
of both triangles.
The total area of the rhomboid equals
(AF)(FC) + (FD)(FC), or (AF + FD)(FC). But
AF + FD equals AD, the base. FC equals the
altitude. Therefore, the formula for the area of
a rhomboid is A = bh. Here again you must
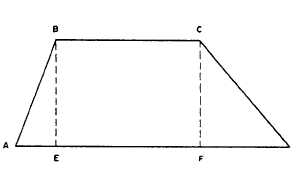
Figure 1-10.-Trapezoid.
remember that h in a rectangle corresponds to the
length of one of the sides, but h in a rhombus or
rhomboid does not.
Area of a Trapezoid
Figure 1-10 shows a trapezoid, ABCD. If you
drop perpendiculars BE and CF from points B
and C, respectively, you create the right triangles
AEB and DFC and the rectangle EBCF between
them. The area of the trapezoid obviously equals
the sum of the areas of these figures.
The area of AAEB equals 1/2(AE)(FC),
the area of ADFC equals 1/2(FD)(FC),
and the area of EBCF equals (EF)(FC). There-
fore, the area of the trapezoid ABCD equals
l/2(AE)(FC) + (EF)(FC) + 1/2(FD)(FC), or
However, 2EF = EF + BC. Therefore, the area
of the trapezoid equals
But AE + FD + EF = AD. Therefore, the area
of the trapezoid equals
AD and BC are the bases of the trapezoid and
are usually designated as bl and b2, respectively.
FC is the altitude and is generally designated as
h. Therefore, the formula for the area of a
trapezoid is
Figure 1-9.-Rhomboid.
1-11