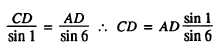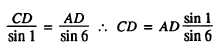form vertically opposite angles 9-10 and 11-12. From
your knowledge of geometry, you know that when two
straight lines intersect the vertically opposite angles
thus formed are equal. From the fact that the sum of the
angles in any triangle is 180°, it follows that for any pair
of vertically opposite angles in figure 15-28, the sums
of the other two angles in each of the corresponding
triangles must be equal.
For example: In figure 15-28, angles 11 and 12 are
equal vertically opposite angles. Angle 11 lies in a
triangle in which the other two angles are angles 1 and
8; angle 12 lies in a triangle in which the other two angles
are angles 4 and 5. It follows, then, that the sum of angle
1 plus angle 8 must equal the sum of angle 5 plus angle
4. By similar reasoning, the sum of angle 2 plus angle 3
must equal the sum of angle 6 plus angle 7.
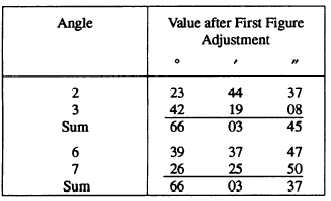
Suppose now, that the values of angles 2, 3, 6, and
7, after adjustment for the sum of interior angles, areas
follows:
The difference between the two sums is 8 seconds.
This means that, to make the sums equal, 4 seconds
should be subtracted from the 2-3 sum and added to the
6-7 sum. To subtract 4 seconds from the 2-3 sum, you
subtract 2 seconds from each angle; to add 4 seconds to
the 6-7 sum, you add 2 seconds to each angle.
The final step in quadrilateral adjustment is related
to the fact that you can compute the length of a side in
a quadrilateral by more than one route. The final step in
adjustment is to ensure that, for a given side, you will
get the same result, to the desired number of significant
figures, regardless of the route your computations take.
This final adjustment is called the log-sine
adjustment, because it uses the logarithmic sines of the
angles. The method is based on the use of side equations
to derive an equation from which the sides are
eliminated and only the sines of the angles remain. This
equation is derived as follows:
Suppose that in figure 15-28, AB is the baseline and
the length of CD is to be computed. By the law of sines,
By the same law,
Substituting the value of AD, we have
Again by the law of sines we have
By the same law,
Substituting this value for BC, we have
We now have two values for CD, as follows:
It follows that
Canceling out AB, we have
By the law of proportions, this can be expressed as
15-36