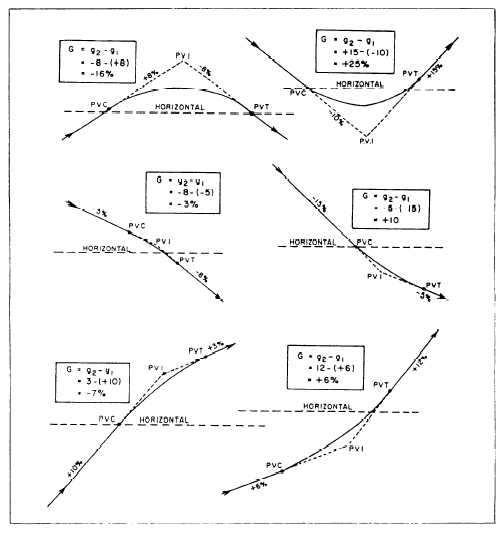
GLThe algebraic difference of the grades:G = g2 -g,,wherein plus values are assigned to uphillgrades and minus values to downhill grades;examples of various algebraic differences areshown later in this section.Length of the curve; the horizontal lengthmeasured in 100-foot stations from the PVC tothe PVT. This length may be computed usingthe formula L = G/r, where r is the rate ofchange (usually given in the design criteria).When the rate of change is not given, L (instations) can be computed as follows: for asummit curve, L = 125 x G/4; for a sag curve,L = 100 x G/4. If L does not come out to a wholenumber of stations using these formulas, thenit is usually extended to the nearest wholenumber. You should note that these formulasfor length are for road design only, NOTrailway.1]Horizontal length of the portion of the PVCto the PVI; measured in feet.12Horizontal length of the portion of the curveform the PVI to the PVT; measured in feet.eVertical (external) distance from the PVI to thecurve, measured in feet. This distance iscomputed using the formula e = LG/8, whereL is the total length in stations and G is thealgebraic difference of the grades in percent.Figure 11-16.—Algebraic differences of grades.11-14
Integrated Publishing, Inc. - A (SDVOSB) Service Disabled Veteran Owned Small Business
