Plotting Horizontal Control

Figure 7-34.Computation of area which includes external area of curves.

PLOTTING ANGLES FROM TANGENTS - 14071_147

Engineering Aid 2 - Intermediate Structural engineering guide book
Page Navigation
131

in this case, because each curve has two tangents rather than a single long chord. The coordinates of A, B, C, and D are the same as in the first example, but the coordinates of the points of intersection (PIs) must be established from the latitudes and departures of the tangents. The computations for determining the tangent bearings are shown in the lower left of figure 7-34. When you have only the chord bearing, you can compute the tangent bearing by adding or subtracting one half of delta (A) as correct. The angle between the tangent and the chord equals N2. After setting coordinates on the PIs, you cross-multiply, accumulate the products, subtract the smaller from the larger, and divide by 2, as before, to get the area of the straight-line figure running around the tangents. You then add or subtract each external area as appropriate. In figure 7-33, you can see that the external area for Curve 1 is inside the parcel boundary and must be added, while that of Curve 2 is outside and must be subtracted. The area comes to 348,881 square feet, which is an acceptable check on the area obtained by using segmental areas. Plotting Horizontal Control Computations for horizontal control become greatly clarified when you can see a plot (that is, a graphic representation to scale) of the traverse on which you are working. A glance at the plot of a closed traverse, for instance, tells you whether you should add or subtract the departure or the latitude of a traverse line in computing the departure or latitude of an adjacent line or in computing the coordinates of a station. For linear distances that are given in feet and decimals of feet, you use the correct scale on an engineer’s scale for laying off linear distances on a plot. For plotting traverses, there are three common methods: by protractor and scale, by tangents, and by coordinates. 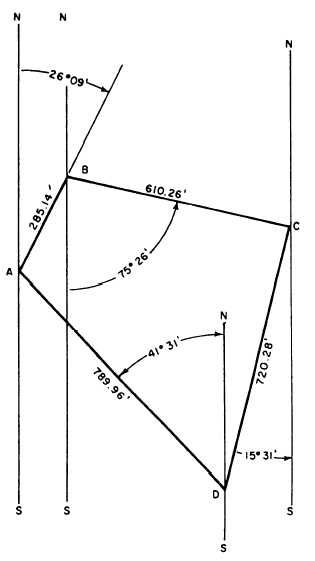PLOTTING ANGLES BY PROTRACTOR AND SCALE.— For the traverse on which you have been working, the adjusted bearings and distances are as follows: Traverse Line Bearing Distance AB N26°09'E 285.14 feet BC S75°26'E 610.26 feet CD S15°31'W 720.28 feet DA N41°31'W 789.96 feet Figure 7-35.—Traverse plotted by protractor-and-scale method. Figure 7-35 shows the method of how to plot this traverse with a scale and protractor. First select a scale that will make the plot fit on the size of your paper. Select a convenient point on the paper for stations A and draw a light line NS, representing the meridian through the station. AB bears N26°9'E. Set the protractor with the central hole on A and the 00 line at NS, and lay off 26°09'E. You will have to estimate the minutes as best you can. Draw a line in this direction from A, and on the line measure off the length of AB (285. 14 feet) to scale. This locates station B on the plot. Draw a light line NS through B parallel to NS through A, and representing the meridian through station B. BC bears S75°26'E. Set the protractor with the central hole on B and the 00 line on NS, lay off 75°26' from the S leg of NS to the E, and measure off the length of BC (610.26 feet) to scale to 7-24

Privacy Statement
Press Release
Contact