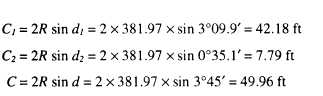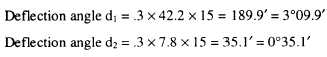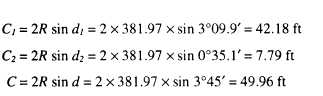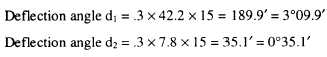From these computed values, we can determine the
stations of the PI, PC, and PT as follows:
By studying figure 11-10 and remembering
that our task is to stake half-station intervals, you
can see that the first half station after the PC is Station
18 + 50 and the last half station before the PT is
23+ 00; therefore, the distance from the PC to Station
18 + 00 is 42.2 feet [(18 + 50) - (18 + 07.80)].
Similarly, the distance from Station 23+ 00 to the PT
is 7.8 feet. These distances are used to compute the
deflection angles for the subchords using the formula
for deflection angles (d= .3CD) as follows:
A convenient method of determining the deflection
angle (d) for each full chord is to remember that d equals
1/2D for 100-foot chords, 1/4D for 50-foot chords, 1/8D
for 25-foot chords, and 1/20D for 10-foot chords. In this
case, since we are staking 50-foot stations, d = 15/4, or
3°45’.
Previously, we discussed the difference in length
between arcs and chords. In that discussion, you
learned that to be within allowable error, the recom-
mended chord length for an 8- to 16-degree curve is
25 feet. Since in this example we are using 50-foot
chords, the length of the chords must be adjusted. The
adjusted lengths are computed using a rearrangement
of the formula for the sine of deflection angles as
follows:
As you can see, in this case, there is little difference
between the original and adjusted chord lengths;
however, if we were using 100-foot stations rather than
50-foot stations, the adjusted difference for each full
chord would be substantial (over 3 inches).
Now, remembering our previous discussion of
deflection angles and chords, you know that all of the
deflection angles are usually turned using a transit that
is set up at the PC. The deflection angles that we turn
are found by cumulating the individual deflection
angles from the PC to the PT as shown below:
Notice that the deflection angle at the PT is equal
to one half of the I angle. That serves as a check of
your computations. Had the deflection angle been
anything different than one half of the I angle, then a
mistake would have been made.
Since the total of the deflection angles should be
one-half of the I angle, a problem arises when the I
angle contains an odd number of minutes and the
instrument used is a 1-minute transit. Since the PT is
normally staked before the curve is run, the total
deflection will be a check on the PC therefore, it
should be computed to the nearest 0.5 degree. If the
total deflection checks to the nearest minute in the
field, it can be considered correct.
The curve that was just solved had an I angle of
75° and a degree of curve of 15°. When the I angle and
degree of curve consists of both degrees and minutes,
the procedure in solving the curve does not change;
but you must be careful in substituting these values
into the formulas for length and deflection angles; for
example I = 42°15’, D = 5°37’. The minutes in each
angle must be changed to a decimal part of a degree.
To obtain the required accuracy, you should convert
them to five decimal places; but an alternate method
for computing the length is to convert the I angle and
degree of curve to minutes; thus, 42°15’ = 2,535 min-
utes and 5°37’ = 337 minutes. Substituting this infor-
mation into the length formula gives the following:
11-9