GM, metacentric height, is the distance from G
Righting moments are measured in foot-tons. Since
the righting arm (GZ) is equal to GM times sin θ, for
to M; it is measured in feet. Z is the point at
small values of θ, you can say that the righting
which a line, through G, parallel to the waterline,
intersects the vertical line through B.
moment is equal to W times GM times sin θ. Because
GZ, the distance from G to Z, is the ship's righting
of the relationship between righting arms and righting
moments, it is obvious that stability may be expressed
arm; it is measured in feet. For small angles of
either in terms of GZ or in righting moments.
heel, GZ may be expressed by the equation
However, you must be very careful not to confuse
GZ = GM sin θ
righting arms with righting moments; they are NOT
W is the weight (displacement) of the ship; it is
identical.
measured in long tons.
STABILITY CURVES
K is a point at the bottom of the keel, at the
midship section, from which all vertical
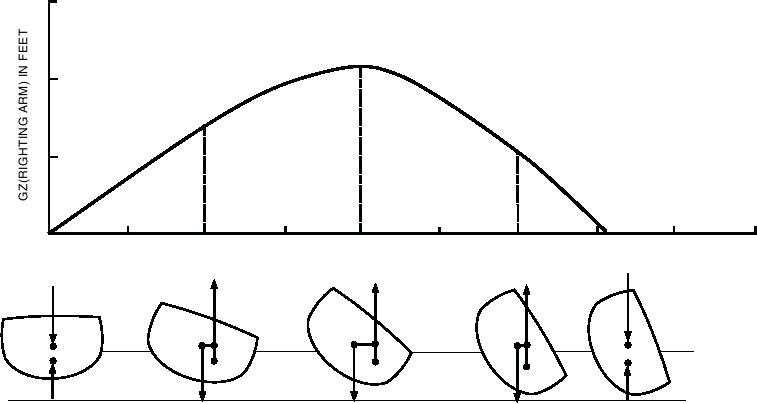
When a series of values for GZ (the ship's righting
measurements are made.
arm) at successive angles of heel are plotted on a graph,
KB is the vertical distance from K to the center of
the result is a STABILITY CURVE. The stability
buoyancy when the ship is upright. KB is
curve, as shown in figure 12-24, is called the CURVE
measured in feet.
OF STATIC STABILITY. The word static indicates
KG is the vertical distance from K to the ship's
that it is not necessary for the ship to be in motion for
the curve to apply. If the ship is momentarily stopped at
center of gravity when the ship is upright. KG is
any angle during its roll, the value of GZ given by the
measured in feet.
curve will still apply.
KM is the vertical distance from K to the
NOTE
metacenter when the ship is upright. KM is
measured in feet.
The stability curve is calculated
The RIGHTING MOMENT of a ship is W times
graphically by design engineers for values
GZ, that is, the displacement times the righting arm.
indicated by angles of heel above 7.
3
2
1
10
20
50
60
30
80
90
40
70
0
ANGLE OF HEEL, IN DEGREES
G
Z
Z
G
G
G
Z
G
WATERLINE
B
B
B
B
B
o
ANGLE OF HEEL = 20
o
o
ANGLE OF HEEL = 40
ANGLE OF HEEL = 0
ANGLE OF HEEL = 60o
o
ANGLE OF HEEL = 70
GZ = 1.33 FEET
GZ = 2.13 FEET
GZ = 0
GZ = 1 FOOT
GZ = 0
DCf1224
Figure 12-24. Curve of static stability.
12-12



