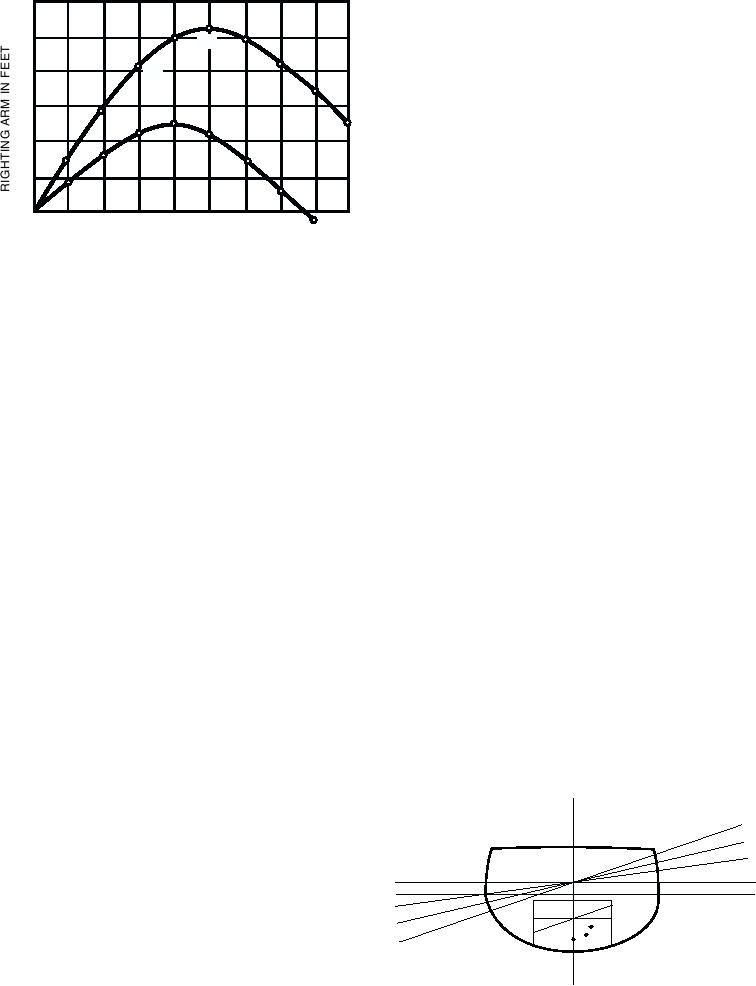
6
At 70, the corrected GZ = 0.5412
At 80, the corrected GZ = minus 0.4392
5
(e)
(d)
(f)
It is not necessary to figure the corrected GZ at 90,
(g)
(c)
4
since the value is already negative at 80. When the
(h)
values from 10 through 80 are plotted on the grid and
3
(b)
joined with a smooth curve, the CORRECTED
A
(i)
stability curve (B) shown in figure 12-27 results. As
2
you can see, the corrected curve shows maximum
(a)
1
stability to be at 40; it also shows that an upsetting
arm, rather than a righting arm, generally exists at
angles of heel in excess of 75.
0
80 90
60
50
30
20
40
70
10
B
ANGLE OF HEEL IN DEGREES
EFFECTS OF LOOSE WATER
DCf1227
When a tank or a compartment in a ship is partially
Figure 12-27. A. Uncorrected stability curve taken from cross
full of liquid that is free to move as the ship heels, the
curves; B. Corrected stability curve.
surface of the liquid tends to remain level. The surface
of the free liquid is referred to as FREE SURFACE.
The tendency of the liquid to remain level as the ship
Suppose that the cross curves are made up on the
heels is referred to as FREE SURFACE EFFECT. The
basis of an assumed KG of 20 feet and that you
term LOOSE WATER is used to describe liquid that has
determine that the actual KG is 24 feet for the particular
a free surface; it is NOT used to describe water or other
condition of loading. This means that the true G is 4 feet
liquid that completely fills a tank or compartment and
higher than the assumed G and that the righting arm
thus has no free surface.
(GZ) at each angle of inclination will be SMALLER
than the righting arm shown in figure 12-27 (curve A)
Free Surface Effect
for the same angle. To find the new value of GZ for each
Free surface in a ship causes a reduction in GM, due
angle of inclination, multiply the increase in KG (4 feet)
to a change in the center of gravity, and a consequent
by the sine of the angle of inclination, and SUBTRACT
reduction in stability. The free surface effect is separate
this product from the value of GZ shown on the cross
from and independent of any effect that may result
curves or on the uncorrected stability curve. In order to
merely from the addition of the weight of the liquid.
facilitate the correction of the stability curves, a table
When free surface exists, a free surface correction must
showing the necessary sines of the angles of inclination
be included in stability calculations. However, when a
is included on the cross curves form.
tank is completely filled so that there is no free surface,
Next, find the corrected values of GZ for the
the liquid in the tank may be treated as a solid; that is, the
various angles of heel shown on the stability curve (A)
only effect of the liquid on stability is the effect of its
in figure 12-27, and plot them on the same grid to make
weight at its particular location.
the corrected stability curve (B) shown in figure 12-27.
To understand the actions that occur because of
free surface effect, use a centerline compartment that is
At 10, the uncorrected value of GZ is 1.4;
partially full of water, as shown in figure 12-28, as an
therefore, the corrected GZ at 10 is 1.4 minus
example.
(4 x 0.1736), or 0.7056.
At 20, the uncorrected value of GZ is 2.8;
L4
therefore, the corrected GZ at 20 is 2.8 minus
L3
(4 x 0.3420), or 1.4320.
L2
L1
W1
Repeating this process at 30, 40, 50, 60, 70,
W
L
W2
and 80, the following values are obtained:
l4
W3
w
l
F
W4
w
At 30, the corrected GZ = 2.2000
E
4
D
At 40, the corrected GZ = 2.3288
At 50, the corrected GZ = 2.2360
DCf1228
Figure 12-28. Effects of free surface.
At 60, the corrected GZ = 1.4360
12-15



