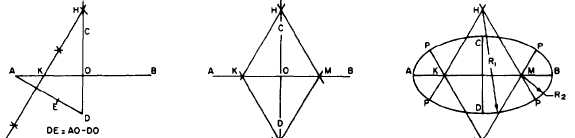
Figure 4-45.-Ellipse by four-center method.
ELLIPSE BY FOUR-CENTER METHOD
The four-center method is used for small
ellipses. Given major axis, AB, and minor axis,
CD, mutually perpendicular at their midpoint, O,
as shown in figure 4-45, draw AD, connecting the
end points of the two axes. With the dividers set
to DO, measure DO along AO and reset the
dividers on the remaining distance to O. With the
difference of semiaxes thus set on the dividers,
mark off DE equal to AO minus DO. Draw
perpendicular bisector AE, and extend it to
intersect the major axis at K and the minor axis
extended at H. With the dividers, mark off OM
equal to OK, and OL equal to OH. With H as
a center and radius R1 equal to HD, draw the
bottom arc. With L as a center and the same
radius as R1, draw the top arc. With M as a center
and the radius R2 equal to MB draw the end arc.
With K as a center and the same radius, R2, draw
the end arc. The four circular arcs thus drawn
meet, in common points of tangency, P, at the
ends of their radii in their lines of centers.
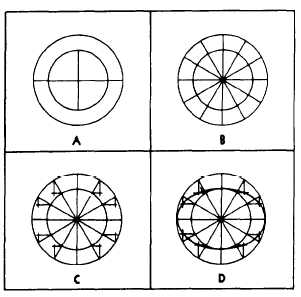
ELLIPSE BY CONCENTRIC-
CIRCLE METHOD
Figure 4-46 shows the concentric-circle method
of drawing an ellipse. With the point of inter-
section between the axes as a center, draw two
concentric circles (circles with a common center),
one with a diameter equal to the major axis and
the other with a diameter equal to the minor axis,
as shown in figure 4-46, view A. Draw a number
of diameters as shown in figure 4-46, view B.
From the point of intersection of each diameter
with the larger circle, draw a vertical line; and
from the point of intersection of each diameter
with the smaller circle, draw an intersecting
horizontal line, as shown in figure 4-46, view C.
Draw the ellipse through the points of inter-
section, as shown in figure 4-46, view D, with a
french curve.
Figure 4-46.-Ellipse by concentric-circle method.
4-16