An arc tangent to two others may enclose
both, or it may enclose only one and not
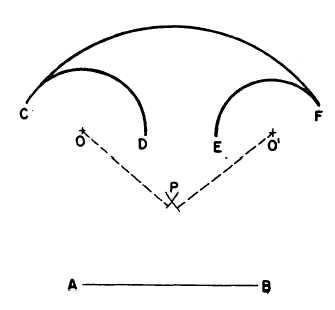
the other. In figure 4-38 the problem is
to draw a circular arc with a radius equal
to AB, tangent to and enclosing both arcs
CD and EF. Set a compass to a radius
equal to AB less the radius of CD (indicated
by the dashed line from O), and, with O
as a center, strike an arc. Set the compass
to a radius equal to AB less the radius
of EF (indicated by the dashed line from
O´), and, with O´ as a center, strike an inter-
secting arc at P. The point of intersection of
these two arcs is the center of a circle of which
an arc of given radius is tangent to, and encloses,
both arcs CD and EF.
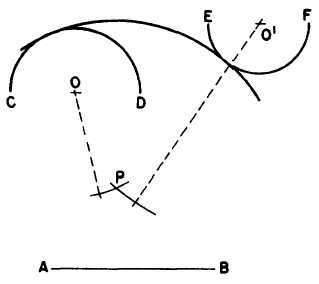
In figure 4-39 the problem is to draw
a circular arc with a radius equal to AB,
tangent to, and enclosing, CD, and tangent
to, but NOT enclosing, EF. Set a compass
to a radius equal to AB less the radius
of arc CD (indicated by the dashed line from
0), and, with O as a center, strike an
arc, Set the compass to AB plus the radius
of EF (as indicated by the dashed line from
O´), and, with O´ as a center, strike an inter-
secting arc at P. The point of intersection of the
two arcs is the center of a circle of which an arc
of the given radius is tangent to and encloses arc
CD and also is tangent to, but does not enclose,
arc EF.
Figure 4-38.-Circular arc tangent to
other circular arcs.
and enclosing two
Figure 4-39.-Circular arc tangent to and enclosing one arc
and tangent to, but not enclosing, another.
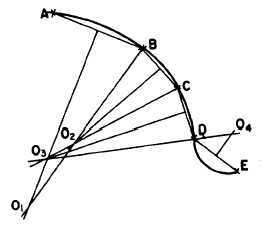
Figure 4-40.-Curve composed of a series of consecutive
tangent circular arcs.
COMPOUND CURVES
A curve that is made up of a series of
successive tangent circular arcs is called a
compound curve. In figure 4-40 the problem is
to construct a compound curve passing through
given points A, B, C, D, and E. First, connect
the points by straight lines. The straight line
between each pair of points constitutes the chord
of the arc through the points.
Erect a perpendicular bisector from AB. Select
an appropriate point O1 on the bisector as a
center, and draw the arc AB. From O1, draw the
4-13