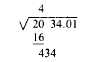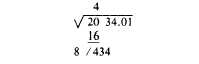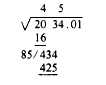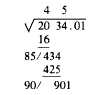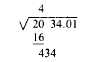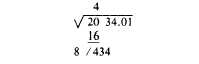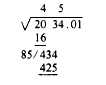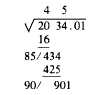extract the denominator, as indicated by the
following example:
The same is true in the division of radicals;
for example,
Any radical expression has a decimal
equivalent, which may be exact if the radicand
is a rational number. If the radicand is not
rational, the root may be expressed as a decimal
approximation, but it can never be exact. A
procedure similar to long division may be used
for calculating square root. Cube root and higher
roots may be calculated by methods based on
logarithms and higher mathematics. Tables of
powers and roots have been calculated for use in
those scientific fields in which it is frequently
necessary to work with roots. Such tables may be
found in appendix I of Mathematics, Vol. 1,
NAVEDTRA 10069-D 1, and in Surveying Tables
and Graphs, Army TM 5-236. This method is,
however, slowly being phased out and being
replaced by the use of hand-held scientific
calculators.
Arithmetic Extraction of Square Roots
If you do not have an electronic calculator,
you may extract square roots arithmetically as
follows:
Suppose you want to extract the square root
of 2,034.01. First, divide the number into
two-digit groups, working away from the decimal
point. Thus set off, the number appears as
follows:
Next, find the largest number whose square
can be contained in the first group, This is the
number 4, whose square is 16. The 4 is the first
digit of your answer. Place the 4 above the 20,
and place its square (16) under the first group,
thus:
Now perform the indicated subtraction and
bring down the next group to the right, thus:
Next, double the portion of the answer already
found (4, which doubled is 8), and set the result
down as the first digit of a new divisor, thus:
The second digit of the new divisor is
obtained by a trial-and-error method. Divide the
single digit 8 into the first two digits of the
remainder 434 (that is, into 43) until you obtain
the largest number that you can (1) add as another
digit to the divisor and (2) use as a multiplier
which, when multiplied by the increased divisor,
will produce the largest result containable in the
remainder 434. In this case, the first number you
try is 43 + 8, or 5. Write this 5 after the 8 and
you get 85. Multiply 85 by 5 and you get 425,
which is containable in 434.
The second digit of your answer is therefore
5. Place the 5 above 34. Your computation will
now look like this:
Proceed as before to perform the indicated
subtraction and bring down the next group, thus:
Again double the portion of the answer
already found, and set the result (45 x 2, or 90)
down as the first two digits of a new divisor thus:
1-5