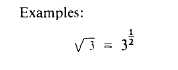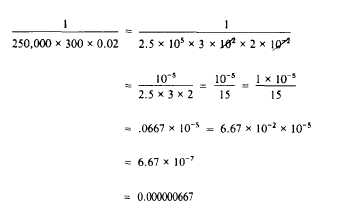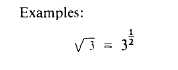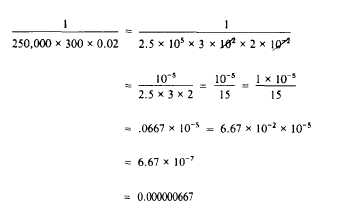Proceed as before to determine the largest
number that can be added as a digit to the divisor
90 and used as a multiplier which, when multiplied
by the increased divisor, will produce a result
containable in the remainder, 901. This number
is obviously 1. The increased divisor is 901, and
this figure, multiplied by the 1, gives a result
exactly equal to the remainder 901.
The figure 1 is therefore the third and final
digit in the answer, The square root of 2,034.01
is therefore 45.1
Your completed computation appears thus:
Fractional and Negative Exponents
In some formulas, like the velocity (V) of
liquids in pipes, which you will encounter later
in Engineering Aid 1 & C, it is more convenient
to use FRACTIONAL EXPONENTS instead of
radicals.
It is readily observed that the index of the root
in the above examples is the denominator of the
fractional exponent. When an exponent occurs in
the radicand,
this exponent becomes the
numerator of the fractional exponent. Roots of
numbers not found in tables may be easily
computed by proper treatment of the radical used.
Examples:
Very small or very large numbers used
in science are expressed in the form 5.832 x 10-4
or 8.143 x 106 to simplify computation. To write
out any of these numbers in full, just move
the decimal point to either left or right, the
number of places equal to the exponent,
supplying a sufficient number of zeros depending
upon the sign of the exponent, as shown below:
RECIPROCALS
The reciprocal of a number is 1 divided by the
number. The reciprocal of 2, for example, is 1/2,
and the reciprocal of 2/3 is 1 divided by 2/3,
which amounts to 1 x 3/2, or 3/2. The reciprocal
of a whole number, then, equals 1 over the
number, while the reciprocal of a fraction equals
the fraction inverted.
In problems containing the power of 10,
generally, it is more convenient to use reciprocals
rather than write out lengthy decimals or whole
numbers.
Example:
1-6