earth’s surface is projected onto a cylinder, and the
conic, in which the surface is projected onto a cone.
A third method is the gnomonic method, in which the
earth’s surface is projected onto a plane placed tangent
to a particular point. For a polar gnomonic chart, this
point is one of the earth’s geographical poles.
MERCATOR PROJECTION
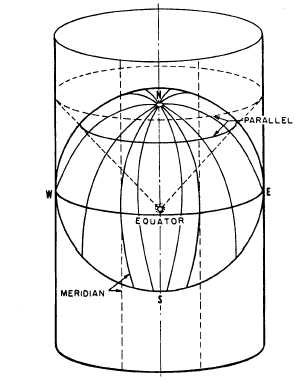
To grasp the concept of Mercator projection,
imagine the earth to be a glass sphere with a strong
light at the center. Imagine, also, that the geographical
meridians and parallels are inscribed as lines on the
sphere at a given interval (for example, every 15
degrees). Now imagine a paper cylinder placed
around the sphere, tangent to the equator, as shown in
figure 9-11. The shadow images of the meridians will
appear on the paper as equally spaced, parallel, verti-
cal lines. The shadow images of the parallels will
likewise appear as straight lines running perpendicu-
lar to the shadow images of the meridians. The paral-
lels are not actually equally spaced, however; instead,
the distance between adjacent parallels will progres-
sively increase as latitude (distance north or south of
the equator, the line of tangency) increases.
Figure 9-11.—Mercator projection.
You can see that there are two elements of
distortion here, each of which progressively increases
with latitude. One is the fact that the meridians, which
on the earth itself converge at each of the poles, are
parallel (and therefore equidistant) for their entire
length on the cylinder. The other is the fact that the
parallels, which are actually equidistant on the sphere
itself, become progressively farther apart as latitude
increases.
These two elements produce the familiar
distortion that is characteristic of a Mercator map of
the world. On such a map the island of Greenland,
which has an area of only about 46,740 square miles,
is considerably larger in outline than the continental
United States, which has an area (excluding Alaska)
of about 2,973,776 square miles.
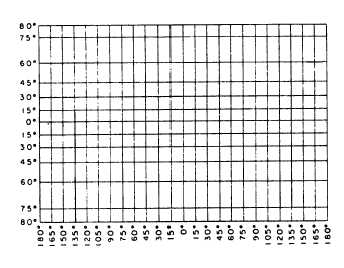
Figure 9-12 shows the meridians and parallels at
15-degree intervals of the earth’s surface on a Merca-
tor projection. Note that the parallels extend only to
80 degrees north and south. Because the cylinder has
no ends, Mercator projection of regions in latitudes
higher than about 80 degrees is impossible. Note, too,
that although the distance along a meridian between
(for example) 15°N and 30°N and between 60°N and
75°N is the same on the ground, these distances are
much different on a Mercator projection. Still another
characteristic to note is the fact that a meridian is
perpendicular to all parallels it intersects and that all
the meridians are parallel to each other.
Transverse Mercator Projection
On a Mercator projection the cylinder is placed
tangent to the earth’s central parallel, the equator. On
Figure 9-12.—Meridians and parallels on a Mercator
projection.
9-11