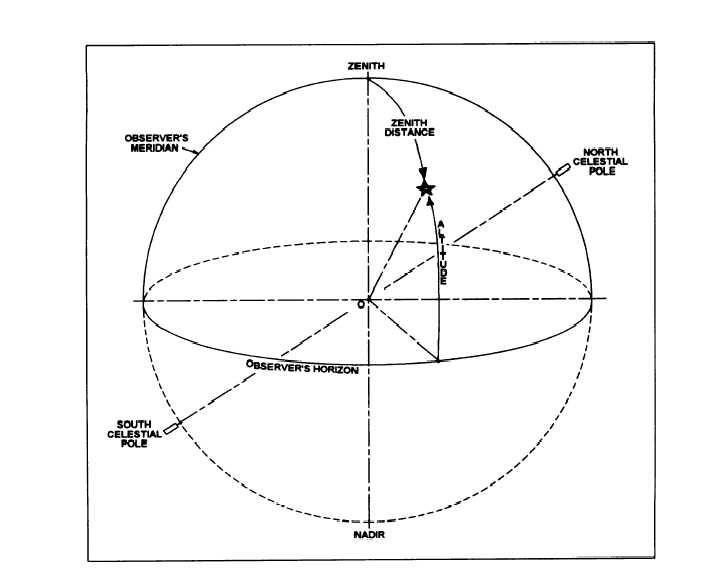
Figure 15-4.-Horizon system of coordinates.
system is the observer’s horizon. Figure 15-4 illustrates
the horizon system. In this figure, O represents both the
earth and the location of the observer.
The horizon is a plane through the observer’s
position that is perpendicular to the direction of gravity
at that point and that intercepts the celestial sphere in a
great circle. The direction of gravity, commonly called
the direction of the plumb line, does not necessarily pass
through the earth’s center. The horizon plane is
considered tangent to the surface of the earth at the
observer’s position For most star observations, the
distance from this plane to the center of the earth is too
small to affect the computations. However, observations
of the sun, planets, and some of the nearer stars, when
used in the more precise computations, must account for
the displacement of the horizon plane. This is called the
correction for parallax.
The point where the plumb line, extended overhead,
pierces the celestial sphere is known as the zenith. The
point opposite this and underneath is the nadir. Great
circles drawn through the zenith and nadir (with their
planes perpendicular to that of the horizon) are called
vertical circles. The angular distance of a celestial body
measured along a vertical circle from the horizon is the
altitude (h) of the body. The complement of the altitude
is the coaltitude, or zenith distance, and is measured
along the vertical circle from the zenith to the body.
The vertical circle through the poles, which also
passes through the zenith, is called the observer’s
meridian. The azimuth of an object is the angle
measured clockwise in the plane of the horizon from the
observer’s meridian to the vertical circle passing
through the object. The northern intersection of the
meridian with the horizon is used as the zero azimuth
15-6