Local Hour Angle (LHA)

Figure 15-6.-Time diagram. - 14071_348

Meridian Angle

Engineering Aid 2 - Intermediate Structural engineering guide book
Page Navigation
328

equinox; you then have the star located on the time diagram. Let’s say it is the star Vega, whose SHA is approximately 81°. Figure 15-9 shows Vega located on the time diagram. Itis easy to see herethat the GHA of Vega must be equal to the GHA of the vernal equinox plus the SHA of Vega (or GHAEL%%, = GHAr + SHAVqa. In this example, the GHA of Vega is 81° plus 45°, or 126°. Now let’s use the time diagram to explain some more facts about nautical astronomy. Local Hour Angle (LHA) Local hour angle (LHA) is the name given to the angle of arc (expressed in degrees, minutes, and tenths of minutes) of the celestial equator between the celestial meridian of a point on the celestial sphere and the hour circle of a heavenly body. It is always measured westward from the local meridian through 360°. Let’s work this problem of LHA on a time diagram. Say you are at longitude 135° from M toward Greenwich which means, of course, that Greenwich will be shown east of M. Think it over for a moment—you are to the west of Greenwich; therefore, Greenwich is to the east of you. 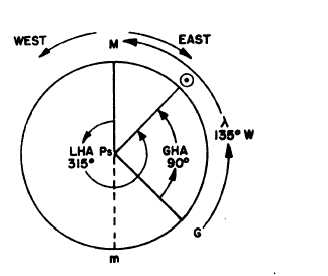Now that we know where Greenwich is and where you are, let’s figure the LHA of the sun as it is shown in figure 15-8. Figure 15-10 shows us that the sun is 90° west of Greenwich. We know that the LHA is always measured westward from your location meridian(M) to the hour circle of the body (in this example, the sun). Therefore, the LHA here is the whole 360° around minus the 45° between the sun’s hour circle and M. This 45° may be found by inspecting figure 15-10 or by subtracting 90° from 135°. Let’s think this over—we are 135°W of Greenwich; therefore, G is 135° clockwise from us. The sun is 90°W or counterclockwise from G. The difference is the 45° we mentioned. Subtract this 45° from 360° and we get 315°, the LHA. Look again at figure 15-10. 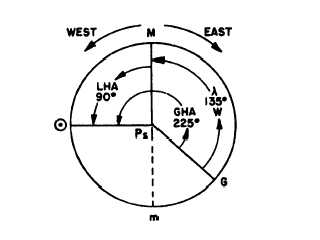As you can see, the sun is east (clockwise on the diagram) of your local meridian (M). Now let’s suppose that you are at the same longitude (135°W), but the GHA of the sun is 225° instead of 90°. The time diagram will appear as shown in figure 15-11. ‘The sun is now west of your meridian (M). The LHA is always measured westward from the local celestial meridian to the hour circle of the body. Therefore, the LHA is the 90° from M to the sun’s hour circle. Here are two general rules that will help you in finding the LHA when the GHA and longitude are known: Figure 15-10.-LHA on the time diagram. Figure 15-11.-LHA with the sun west of your celestial meridian. 1. LHA= GHA– AW (used when longitude is west) 2. LHA = GHA + kE (used when longitude is east) In west longitude it may be necessary to add 360° to the GHA before the subtraction can be made. In east longitude, 360° is subtracted from the LHA if it exceeds this amount. Be sure, however, to check the accuracy of your work by referring to a time diagram. It offers a graphic means of obtaining the data you need. As an illustration, suppose the GHA of the sun is and the longitude is 79°15’05”E. Since longitude is east, you use formula 2 above. Transposing to solve for the LHA, you have 15-13

Privacy Statement
Press Release
Contact