A reduction in the size of the righting arm usually
To understand this stability curve, it is necessary to
consider the following facts:
means a decrease in stability. When the reduction in GZ
is caused by increased displacement, however, the total
1. The ship's center of gravity does NOT change
effect on stability is more difficult to evaluate. Since the
position as the angle of heel is changed.
RIGHTING MOMENT is equal to W times GZ, it will
2. The ship's center of buoyancy is always at the
be increased by the gain in W at the same time that it is
geometric center of the ship's underwater hull.
decreased by the reduction in GZ. The gain in the
righting moment, caused by the gain in W, does not
3. The shape of the ship's underwater hull changes
necessarily compensate for the reduction in GZ.
as the angle of heel changes.
In summary, there are several ways in which an
If these three facts are considered collectively, you
increase in displacement affects the stability of a ship.
will see that the position of G remains constant as the
Although these effects occur at the same time, it is best
ship heels through various angles, but the position of B
to consider them separately. The effects of increased
changes according to the angle of inclination. When
displacement are the following:
the position of B has changed so that B and G are not in
the same vertical line, a righting arm GZ must exist.
1. RIGHTING ARMS (GZ) are decreased as a
The length of this righting arm depends upon the angle
result of increased draft.
at which the ship is inclined (fig. 12-25). GZ increases
2. R I G H T I N G M O M E N T S ( f o o t - t o n s ) a r e
as the angle of heel increases, up to a certain point. At
decreased as a result of decreased GZ.
about an angle of 40, the rate of increase of GZ begins
to level off. The value of GZ diminishes and finally
3. RIGHTING MOMENTS are increased as a
reaches zero at a very large angle of heel.
result of the increased displacement (W).
Cross Curves of Stability
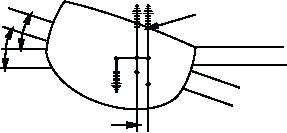
The position of the center of buoyancy at any given
FORCE OF BUOYANCY AT
18 FOOT DRAFT AND 20o HEEL
angle of inclination depends upon the draft. As the
o
20
26 FOOT WATERLINE AT 20o ANGLE OF HEEL
draft increases, the center of buoyancy moves closer to
Z
26
o
20
Z18
18 FOOT WATERLINE AT 20o ANGLE OF HEEL
G
the center of gravity, thereby reducing the length of the
B
26 F
26
OOT
WAT
righting arms. To determine this effect, the design
B 18
ERL
18 F
INE
OO
AT E
TW
VEN
ATE
activity inclines a line drawing of the ship's lines at a
RLI
KEE
NE
L
AT E
VEN
FORCE OF BUOYANCY AT
given angle, and then lays off a series of waterlines on
KEE
26 FOOT DRAFT AND 20oHEEL
L
it. These waterlines are chosen at evenly spaced drafts
DCf1225
throughout the probable range of displacements. For
each waterline the value of the righting arm is
calculated, using an ASSUMED center of gravity,
Figure 12-25. Effect of draft on righting arm.
rather than the TRUE center of gravity. A series of such
c a l c u l a t i o n s i s m a d e f o r va r i o u s a n g l e s o f
heel--usually 10, 20, 30, 40, 50, 60, 70, 80,
Effect of Draft on Righting Arm
and 90--and the results are plotted on a grid to form a
series of curves known as the CROSS CURVES OF
A change in displacement will result in a change of
STABILITY.
draft and freeboard; and B will shift to the geometric
center of the new underwater body. At any angle of
Figure 12-26 is an example of a set of cross curves.
Note that, as draft and displacement increase, the
inclination, a change in draft causes B to shift both
curves all slope downward, indicating increasingly
horizontally and vertically with respect to the keel. The
smaller righting arms.
horizontal shift in B changes the distance between B
and G, and thereby changes the length of the righting
The cross curves are used in the preparation of
arm, GZ. Thus, when draft is increased, the righting
stability curves. To take a stability curve from the cross
arms are reduced throughout the entire range of
curves, draw a vertical line (such as line MN in
stability. Figure 12-25 shows how the righting arm is
fig. 12-26) on the cross curve sheet at the displacement
reduced when the draft is increased from 18 feet to 26
that corresponds to the mean draft of the ship. At the
feet when the ship is inclined at an angle of 20.
intersection of this vertical line with each cross curve,
12-13

