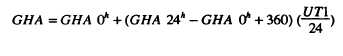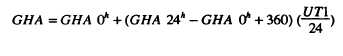where: Z  = LHA  = 6 = a = azimuth of the sun measured clockwise  from  north local hour angle of the sun declination of the sun latitude  of  the  observer Z  is  normalized  from  0°  to  360° algebraically a correction as listed below. by  adding The  above  equation  is  derived  using  spherical trigonometry  to  solve  the  pole-zenith-star  (PZS)  triangle for  azimuth Time and Date To calculate the LHA of the apparent sun at the instant of observation, you must have accurate time that takes into account the rotation of the earth. Time that is based on the rotation of the earth can be obtained by adding  a  correction  factor  to  Greenwich  meantime. Coordinated  universal  time  (UTC)  is  another name for Greenwich mean time and is broadcast by the National  Bureau  of  Standards  on  radio  station  WWV. (Inexpensive  receivers  that  are  pretuned  to  WWV  are available.) The correction factor (designated DUT) that you must add to the coordinated universal time is also obtained from WWV by counting the number of double ticks  following  the  minute  tone.  Each  double  tick represents  a  tenth-of-a-second  correction  and  is  positive the frost 7 seconds (ticks). Beginning with the ninth second,  each  double  tick  is  a  negative  correction.  The total correction, either positive or negative, will not exceed 0.7 second. By adding DUT to UTC, you get time  (designated  UT1)  that  is  based  on  the  actual rotation of the earth. A stopwatch with a split (or lap) time feature is ideal for obtaining times of pointings. The stopwatch is set by starting it on a WWV minute tone and then checking it 1 minute later with a split time. If a significant difference is observed, start and check the stopwatch again. Split times are taken for each pointing on the sun and added to the beginning UTC time, corrected to UT1. To enter the ephemeris tables, you must know the Greenwich date for the time of observation. For an afternoon  observation  (local  time)  in  the  Western Hemisphere, if the UT1 is between 12 and 24 hours, the Greenwich date is the same as the local date. If the UT1 time is between 0 and 12 hours, the Greenwich date is the local date plus 1 day. For  a  morning  observation  (local  time)  in  the Eastern Hemisphere, if the UT1 time is between 0 and 12, the Greenwich date is the same as the local date. If the UT1 time is between 12 and 24 hours, the Greenwich date is the local date minus 1 day. For  a  morning  observation  in  the  Western Hemisphere and an afternoon observation in the Eastern Hemisphere,  Greenwich  and  local  dates  are  the  same. Latitude  and  Longitude Both  the  observer’s  latitude  and  longitude  are required for the hour angle method. Usually these values can be readily obtained by scaling from a map, such as a  USGS  7.5-minute  quadrangle  sheet.  For  sun observations, locating the observer’s position on the map and scaling must be performed to a reasonably high degree  of  accuracy. Declination of the Sun Declination  (6) of the  sun is tabulated for O hours universal time of each day (Greenwich date) in table 15-5.  You  can  interpolate  for  at  the  UT1  time  of observation by using the following equation: A  negative  declination  indicates  that  the  sun  is  south of the equator, and a negative value must be used in the above equation and in the azimuth (Z) equation. The Greenwich hour angle (GHA) of the sun is tabulated  for  0  hours  universal  time  of  each  day (Greenwich date) in the ephemeris. Interpolation is required at the UT1 time of observation and can be accomplished by using the following equation: NOTE: The value at the beginning of the day of observation  is  d’.  The  value  24  hours  later  at  the beginning of the next day is 24h. 15-18