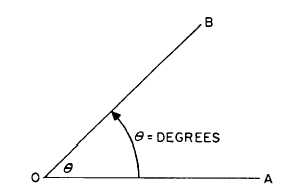
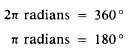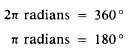Figure 1-19.-Generation of an angle, resulting angle
measured in degrees.
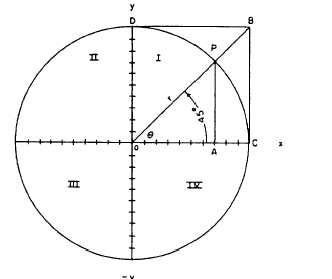
90° sectors, called QUADRANTS, are numbered
counterclockwise starting at the upper right-hand
sector.
When the unit radius r (the line generating the
angle) has traveled less than 90° from its starting
point in a counterclockwise direction (or, as
conventionally referred to as, in a positive
direction), the angle is in the FIRST quadrant (I).
When the unit radius lies between 90° and 180°,
the angle is in the SECOND quadrant (II). Angles
between 180° and 270° are said to lie in the
THIRD quadrant (III), and angles greater than
270° and less than 360° are in the FOURTH
quadrant (IV).
When the line generating the angle passes
through more than 360°, the quadrant in which
the angle lies is found by subtracting from the
angle the largest multiple of 360 that the angle
contains and determining the quadrant in which
the remainder falls.
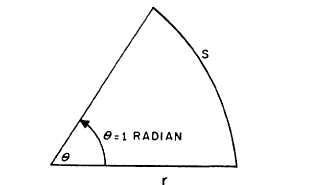
The RADIAN SYSTEM of measuring angles
is even more fundamental than the degree system.
It has certain advantages over the degree system,
for it relates the length of arc generated to the size
of the angle and the radius. The radian measure
is shown in figure 1-20. If the length of the arc
(s) described by the extremity of the line segment
generating the angle is equal to the length of the
line (r), then it is said that the angle described is
exactly equal to one radian in size; that is, for one
radian, s = r.
The circumference of a circle is related to the
radius by the formula, C = 2nr. This says that
the circumference is 2rt times the length of the
radius. From the relationship of arc length,
radius, and radians in the preceding paragraph,
this could be extended to say that a circle
Figure 1-20.-Radian measure.
Figure 1-21.-Circle of unit radius with quadrants shown.
contains 2rr radians, and the circumference
encompasses 3600 of rotation. It follows that
By dividing both sides of the above equation
by n, we find that
As in any other formula, you can always
convert radians to degrees or vice versa by using
the above relationship.
FUNCTIONS OF ANGLES
The functions of angles can best be illustrated
by means of a “circle of unit radius” like the one
shown in figure 1-21. A so-called “Cartesian axis”
1-17