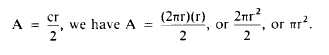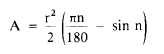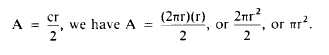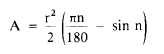Area of a Circle
Figure 1-11.-Trapezium.
Figure 1-12.-Area of a circle.
Stated in words,
equal to one-half
altitude.
the area of a trapezoid is
the sum of its bases times its
Area by Reducing to Triangles
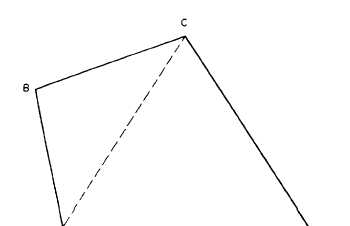
Figure 1-11 shows you how you can determine
the area of a trapezium, or of any polygon,
by reducing to triangles. The dotted line
connecting A and C divides the figure into the
triangles ABC and ACD. The area of the
trapezium obviously equals the sum of the areas
of these triangles.
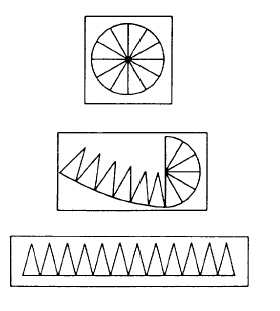
Figure 1-12 shows how you could cut a
disk into 12 equal sectors. Each of these
sectors would constitute a triangle, except for
the slight curvature of the side that was originally
a segment of the circumference of the disk. If
this side is considered the base, then the altitude
for each triangle equals the radius (r) of the
original disk. The area of each triangle, then,
equals
and the area of the original disk equals the sum
of the areas of all the triangles. The sum of the
areas of all the triangles, however, equals the sum
of all the b’s, multiplied by r and divided by 2.
But the sum of all the b’s equals the
circumference (c) of the original disk. Therefore,
the formula for the area of a circle can be
expressed as
However, the circumference of a circle equals the
product of the diameter times n (Greek letter,
pronounced “pi”). n is equal to 3.14159. . . The
diameter equals twice the radius; therefore, the
circumference equals 2rrr. Substituting 2rrr for
c in the formula
This is the most commonly used formula for the
area of a circle. If we find the area of the circle
in terms of circumference.
Area of a Segment and a Sector
A segment is a part of a circle bounded by a
chord and its arc, as shown in figure 1-13. The
formula for its area is
where r = the radius and n = the central angle
in degrees.
1-12