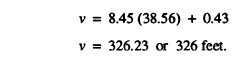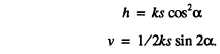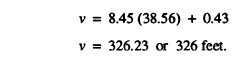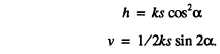values of 100 cos2a and 1/2(100) sin 2a are already
computed at 2-minute intervals for angles up to 30°. You
need to multiply the values in the table by the stadia
reading, then add the value of the instrument constant
given at the bottom of the page.
To find the values from the stadia table, for the
example that we have been discussing, read under 25°
and opposite 14’. Under Hor. Dist. you find that
100 COS2 25°14’ = 81.83.
Under Diff. Elev. you see that
1/2 (100) sin 2 (25014’) = 38.56.
The values of the term containing the instrument
constant are given at the bottom of the page.
For
You find
Therefore
Using these values in the formulas, you have
and
APPROXIMATE FORMS OF STADIA
FORMULAS.— Because of the errors common in
stadia surveying, it has been found that approximate
stadia formulas are precise enough for most stadia work
If you will refer again to figures 8-5 and 8-6, you will
notice that it is customary to hold the stadia rod plumb
rather than inclined at right angles to the line of sight.
Failure to hold the rod plumb introduces an error causing
the observed readings to be longer than the true
readings. Another error inherent in stadia surveying is
caused by the unequal refraction of light rays in the
layers of air close to the earth’s surface. The refraction
error is smallest when the day is cloudy or during the
early morning or late afternoon hours on a sunny day.
Unequal refraction, also, causes the observed readings
to be longer than the true readings.
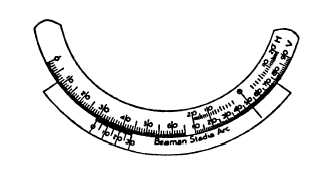
Figure 8-7.-Stadia arc (multiplier type).
Figure 8-8.-Stadia arc (horizontal scale subtraction type).
To compensate for these errors, topographers often
regard the instrument constant as zero in stadia
surveying of ordinary precision, even if the instrument
has an externally focusing telescope. In this way, the last
terms in the stadia formulas for inclined sights vanish;
that is, become zero. Then the approximate
expressions for horizontal and vertical distance are
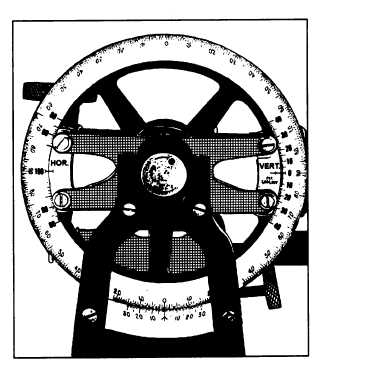
BEAMAN STADIA ARC.— The Beaman stadia
arc is a specially graduated arc on the vertical scale of
the transit (fig. 8-7) or on the plane-table alidade (fig.
8-8). The Beaman arc on the transit is also known as the
stadia circle. These arcs are used to determine distances
and differences in elevation by stadia without using
vertical angles and without using tables or diagrams. A
stadia arc has no vernier, but readings are indicated by
index marks.
8-7