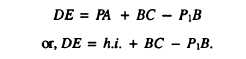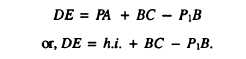The stadia arc shown in figure 8-7 is the  multiplier stadia arc (the vertical index is at zero); that is, the observed stadia interval is multiplied by the  Hor  stadia arc reading to get the horizontal distance; or the stadia interval is multiplied by the Vert stadia arc reading to obtain  the  vertical  distance  from  the  center  of  the instrument to the point sighted on the rod This vertical distance, combined with the HI and the rod reading, will give  the  difference  in  elevation  between  the  instrument station and the point where the rod is held The stadia arc, as shown is figure 8-8, is called the horizontal scale subtraction stadia arc (the vertical index is at 50). The use of the Beaman stadia arc to obtain a horizontal distance and difference in elevation is explained in the following sections. Horizontal Distance (Subtraction Scale).—  The H scale gives you a percentage that you can apply to an inclined  stadia  shot  with  the  alidade  to  get  the corresponding  horizontal  distance  from  the  slope distance.  Suppose  that  with  the  telescope  inclined  (that is, at a vertical angle other than 0°), you read an interval of 2.45 feet on the stadia rod. The slope distance, then What is the corresponding horizontal distance? You read the graduation indicated by the Beaman arc indicator on the H scale, and find that the reading is 5. This means that the horizontal distance is 5 percent less than the slope distance, or 245 feet  – (0.05  x  245  feet),  or 245  –  12.25  =  232.8  feet. Difference  in  Elevation  (Vertical  Index  at 50).—  The  V scale  on  the  Beaman  arc  is  used  to determine  the  difference  in  elevation  between  the elevation of the line of sight through the telescope (that is, the HI) and the elevation of the point you sighted on the level rod Note that when the telescope is horizontal, the  V  scale  on  the  Beaman  arc  reads  50.  This arrangement makes the use of minus values unnecessary when you are sighting with the telescope at a negative vertical angle. To read the V scale, you take the difference between 50 and whatever you read on the scale and apply this difference as follows to determine the difference in elevation. Suppose  that  when  you  made  the  shot  previously described (where you read 5 on the  H scale), the reading on the V scale was 71. In practice, it is the custom to shoot the rod at a point that will give you an even reading on the V scale. Because the reading was 71, the value you will use is 71 –50, or 21%. This means that the difference in elevation between the HI and the point you sighted on the rod is 21 percent of the slope distance. The slope distance, in this case, was 245.0 feet; therefore, the difference in elevation is 245.0 x 0.21 = 51.45 feet. Now that you know how to read stadia and compute horizontal and vertical distances using stadia, we will now  discuss  typical  field  procedures. Field Procedures Figure  8-9  shows  two  situations  that  are encountered in transit-stadia work First, let us discuss the common situation in which you desire to determine the difference in elevation between an instrument station of known elevation and a ground point of unknown elevation. This situation is shown in figure 8-9, view A. In this view, the elevation of the instrument station  P is known and it is desired to determine the difference in elevation   between   P and  the  rod  station  P₁. The horizontal center-line height of the instrument (h.i.) above point P is equal to PA. As you can see, this h.i. is different than the HI that you are accustomed to working with indirect leveling. The rod reading is  P₁B. From your studies, you know that the difference in elevation (DE) between P and P₁ can be expressed as follows: Therefore, the ground elevation at  P₁ can  be  expressed as  follows: Now let us sight on the rod such that P₁B = PA = h.i. In this case, the situation occurs in which a similar triangle (PC₁P₁) is formed at the instrument station P. From observation of these similar triangles, you can see that the DE= P₁C₁ = BC. Therefore,  the  ground  elevation  at P₁ can be simply expressed as follows: This  is  an  important  concept  to  understand  when shooting  stadia  from  a  station  of  known  elevation  As 8-8