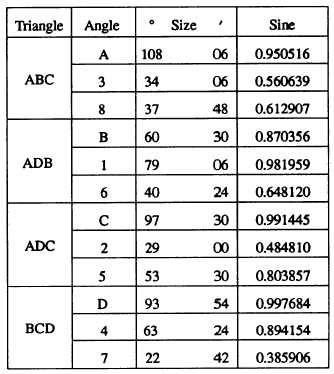
Figure 15-17.—Chain of quadrilaterals.
triangles ADB, ADC, CDE, and EDF, in that order, or
by solving triangles ADB, BDF, and FDE, in that order.
You can also see that this system can be used to cover a
wide territory. It can cover an area extending up to
approximately 25,000 yards in length or breadth.
Chain of Quadrilaterals
A quadrilateral, too, is technically a polygon; and a
chain of quadrilaterals would be technically a chain of
polygons. However, with reference to triangulation
figures, the term chain of quadrilaterals refers to a
figure arrangement like that shown in figure 15-17.
Within each of the quadrilaterals shown, the triangles on
which computations are based are not the four adjacent
triangles visible to the eye, but four overlapping
triangles—each of which has as sides two sides of the
quadrilateral and one diagonal of the quadrilateral. For
example, in quadrilateral ACDB there are four
overlapping triangles as follows: ADC, ADB, ABC, and
BCD. You can see that solving these four triangles will
give you two computations for the length of each
unknown side of the quadrilateral.
Consider, for example, the quadrilateral ACDB.
Look at angle BAC. We will call the whole angle at a
comer by the letter (as, angle A) and a less-than-whole
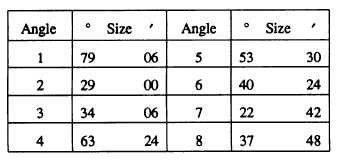
angle at a corner by the number shown (as, angle 1). The
angles at each station on the quadrilateral, as measured
with a protractor to the nearest 0.5 degree and estimated
to the nearest 0.1 degree, are sized as follows:
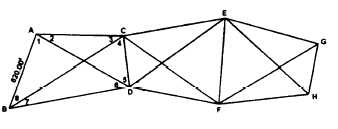
The angles that make up each of the four
overlapping triangles, together with their natural sines,
are as follows:
Note that the total sum of the angles is 360°, which
it should be for a quadrilateral, and that the sum of the
angles in each triangle is 180°, which is also
geometrically correct.
To solve the quadrilateral, you solve each of the
overlapping triangles. First, you solve triangle ABC for
sides AC and BC, using the law of sines as follows:
Then, using similar computation procedures, you
solve triangle ABD for sides BD and AD, triangle ADC
15-26