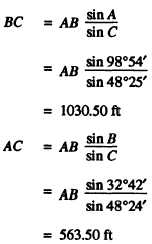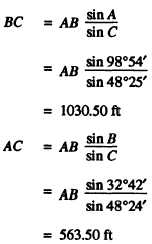Figure 15-15.-Chain of single triangles.
high-order triangulation network to establish control
across the United States.
TYPES OF TRIANGULATION NETWORKS
In triangulation there are three types of triangulation
networks (or nets). They are the chain of single
triangles, chain of polygons, and chain of quadri-
laterals.
Chain of Single Triangles
The simplest triangulation system is the chain of
single triangles shown in figure 15-15. Suppose AB is
the base line and measures 780.00 feet in length.
Suppose, also, that angle A (that is, the observed angle
BAC) measures 98°54´ and that angle ABC measures
32°42´. (In actual practice you will use more precise
values than these; we are using rough values to simplify
the explanation.) Subtracting the sum of these two
angles from 180°, we get 48°24´ for angle ACB.
Next, solve for sides BC and AC by using the law
of sines as follows:
Now that you know how to find the length of BC,
you can proceed in the same manner to determine the
lengths of BD and CD. Knowing the length of CD, you
can proceed in the same manner to determine the lengths
of CE and DE, knowing the length of DE, you can
determine the lengths of DF and EF, and so on. You
should use this method only when locating inaccessible
points, not when a side of the triangle is to be used to
extend control.
In comparison with the other systems about to be
described, the chain of single triangles has two
disadvantages. In the first place, it can be used to cover
only a relatively narrow area. In the second place, it
provides no means for cross-checking computed
distances using computations made by a different route.
In figure 15-15, for example, the only way to compute
the length of BC is by solving the triangle ABC, the only
way to compute the length of CD is by solving the
triangle BCD (using the length of BC previously
computed); and so on. In the systems about to be
described, a distance maybe computed by solving more
than one series of triangles.
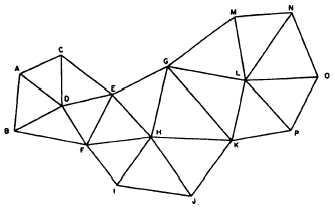
Chain of Polygons
Technically speaking, of course, a triangle is a
polygon; and therefore a chain of single triangles could
be called a chain of polygons. However, in reference to
triangulation figures, the term chain of polygons refers
to a system in which a number of adjacent triangles are
combined to forma polygon, as shown in figure 15-16.
Within each polygon the common vertex of the triangles
that compose it is an observed triangulation station
(which is not the case in the chain of quadrilaterals
described later).
You can see how the length of any line shown can
be computed by two different routes. Assume that AB is
the base line, and you wish to determine the length of
line EF. You can compute this length by solving
Figure 15-16.—Chain of polygons.
15-25