180°00´00´´ – (42°19´08´´ + 44°51´59´´ + 47°28´43´´), or
S45°20´10´´W. The bearing of CD is equal to angle C
minus the bearing angle of BC.
Coordinates
Suppose that you are tying the quadrilateral shown
in figure 15-29 into a state grid system. The nearest
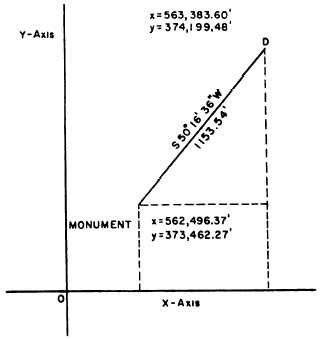
monument in this system lies 1,153.54 feet from
station D, bearing S50°16´36´´W from D, as shown in
figure 15-30. This means that the bearing from the
monument to D is N50°16´36´´E. Suppose that the grid
coordinates of the monument are y = 373,462.27 feet
and x =562,496.37 feet.
The latitude of the line from the monument to
station D is 1,153.54 cos 50°16´36´´, or 737.21 feet. The
departure of the same line is 1,15354 sin 50°16´36´´, or
Figure 15-30.—Coordinates.
You would find the bearing of BC and CD similarly,
except that you have to watch for the angle you are after.
Always remember that a bearing angle does not exceed
90° and is always reckoned from north or south. To
find the bearing of BC, you must find the sum of
angle B (angles 3 and 4, fig. 15-28) plus the bearing
angle of AB and then subtract it from 180°; you can
see that BC bears southwest, so just add this
designation to the proper place in the bearing angle
for BC. In this case, the bearing of BC will be
887.23 feet.
The y coordinate of station D equals the y
coordinate of the monument plus the latitude of the line
from the monument to D, or 373,462.27 + 737.21, or
374,199.48 feet. The x coordinate of station D equals the
x coordinate of the monument plus the departure of the
line from the monument to D, or 562,496.37 + 887.23,
or 563,383.60 feet.
Knowing the coordinates of station D, you can now
determine the coordinates of station A. The latitude of
DA is 700.00 cos 15°00´00´´, or 676.15 feet. The
departure of DA is 700.00 sin 15°00´00´´, or 181.17 feet.
The y coordinate of station A is equal to the y
coordinate of station D plus the latitude of DA, or
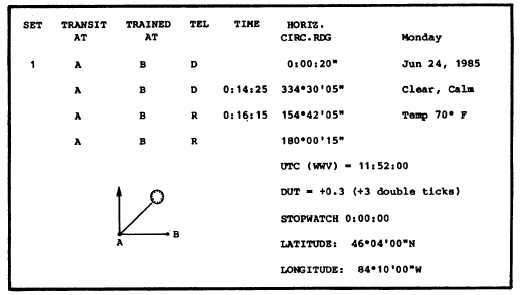
Figure 15-31.—Sun observation field notes.
15-40