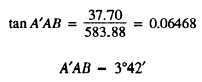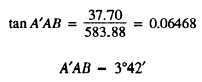Finally, for the 0.32 foot, look up the latitude for
32 feet, which is 30.84 feet. If the latitude for 32 feet is
30.84 feet, the latitude for 0.32 foot must be 0.3084 fret,
which rounds off at 0.31 foot. The numerical value of
the latitude then is 698.59 + 0.31 = 698.90 feet. Because
the line AB bears northeast, the latitude is positive.
You get the departure in the same way by using the
departure column.
Finally, you enter the adjusted latitudes and adjusted
departures in the last two columns. Determine the values
in each case by applying the correction to the original
latitude or departure. Note that the negative latitudes
now equal the positive latitudes and the negative
departures equal the positive departures. This indicates
that the errors of closure have been entirely distributed.
With the adjusted latitudes and departures, you can
now adjust the original bearings and distances by the
method called inversing. Inversing simply means
computing the bearing and length of a traverse line from
the latitude and departure. Again the process is one of
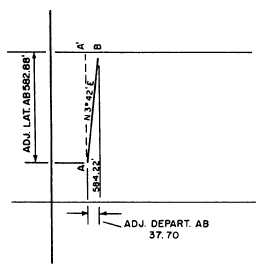
simple triangle solution. Figure 7-16 shows traverse line
AB with the adjusted latitude and departure noted. To
determine the adjusted angle of bearing, you solve the
triangle AA'B for angle A'AB as follows:
The adjusted bearing of AB, then, is N3°42'E. For
the adjusted distance, solve the triangle for AB as
follows:
Figure 7-16.—Adjusted bearing and distance from adjusted
latitude and departure.
The adjusted length of AB, then, is 584.22 feet.
Plane Coordinates
The location of a point by plane coordinates means
to describe the location of the point in terms of its
distance north or south and east or west from a point of
origin.
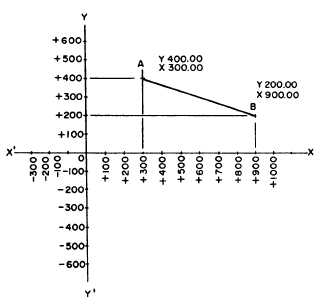
Figure 7-17 shows how coordinate distances are
measured on an axis (called the Y axis) running north to
south through the point of origin. East to west
coordinates are measured on an X axis running east to
west through the point of origin. Values on the Y axis
north of the point of origin are plus; values south of the
point of origin are minus. Values on the X axis east of
the point of origin are plus; values west of the point of
origin are minus.
PLANE COORDINATES FROM LATITUDE
AND DEPARTURE.— Figure 7-17 also shows the
relationship between the plane coordinates of the end
stations on a traverse line and the latitude and departure
of the line. You can see that the difference between the
Y coordinate of A and the Y coordinate of B (which is
200.00 feet) equals the latitude of AB. Also, you can see
that the difference between the X coordinate of A and
the X coordinate of B (which is 600.00 feet) equals the
departure of AB. Therefore, if you know the coordinates
of one of the stations in a traverse, you can determine
the coordinates of the others from the latitudes and
Figure 7-17.—Location by plane coordinates.
7-13