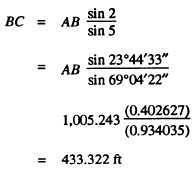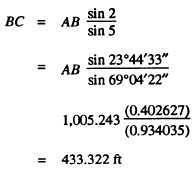.
You can compute the length of BC by (1) solving
The sum of the angles that make up each of the
overlapping triangles within the quadrilateral is as
follows:
The sum of the closing errors for the four triangles
is (09 + 01 + 07 + 01), or 18 seconds. The average
triangle closure for the four triangles, then, is 18/4, or
04.5 seconds. For third-order triangulation, the
maximum average triangle closure is 05 seconds;
therefore, for the third-order work this closure would
be acceptable.
Base Line Discrepancy
If AD is the base line in figure 15-28, then BC would
be the adjacent baseline. assume that the baseline
AD measures 700.00 feet and compute the length of BC
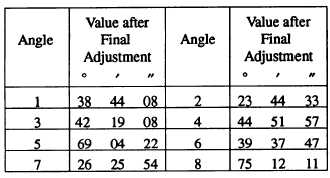
on the basis of the angles we have adjusted. These angles
now measure as follows:
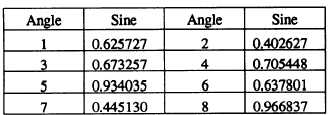
The natural sine of each of these angles is as
follows:
triangle ABD for AB and triangle ABC for BC and (2)
solving triangle ACD for DC and triangle DBC for BC.
Using the law of sines and solving triangle ABD for
side AB, we have
Solving triangle ABC for side BC, we have
Solving triangle ACD for side CD, we have
Solving triangle DBC for side BC, we have
15-38