You know that in logarithms, instead of multiplying
you just add logarithms; also, instead of dividing one
number by another, you just subtract the logarithm of
the second from the logarithm of the first. Note that the
logarithm of 1 is 0.000000. Therefore, the above
equation can be expressed as follows:
(log sin 1 + log sin 3 + log sin 5 + log sin7) - (log sin 2
+ log sin 4 + log sin 6 + log sin 8) = 0
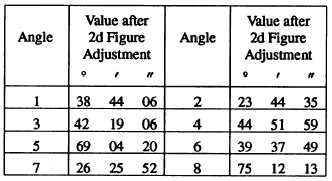
Suppose, now, that after the second figure adjust-
ment, the values of the angles shown in figure 15-28 are
as follows:
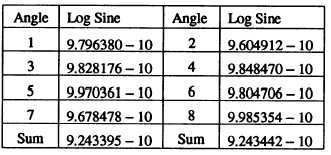
A table of logarithmic functions shows the log sines
of these angles to be as follows:
By subtracting the two sums, you get the following:
9.243442–10
-9.243395–10
0.000047
Therefore, the difference in the sums of the log sines is
0.000047. Since there are eight angles, this means the
average difference for each angle is 0.0000059.
The next question is how to convert this log sine
difference per angle into terms of angular measurement
To do this, you first determine, by reference to the table
of log functions, the average difference in log sine, per
second of arc, for the eight angles involved. This is
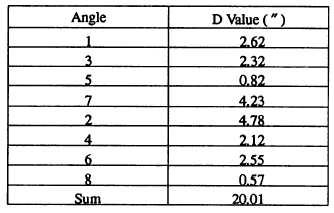
determined from the D values given in the table. For
each of the angles shown in figure 15-28, the D value is
as follows:
The average difference in log sine per 1 second of
arc, then, is 20.01/8, or 2.5. The average difference in
log sine is 5.9; therefore, the average adjustment for
each angle is 5.9 +2.5, or about 2 seconds. The sum of
the log sines of angles 2, 4, 6, and 8 isS greater than that
of angles 1, 3, 5, and 7. There for, you add 2 seconds
each to angles 1, 3, 5, and 7 and subtract 2 seconds each
from angles 2, 4, 6, and 8.
CHECKING FOR PRECISION
Early in this chapter the fact was stated that the
precision of a triangulation survey may be classified
according to (1) the average triangle closure and (2) the
discrepancy between the measured length of a base line
and its length as computed through the system from an
adjacent base line.
Average Triangle Closure
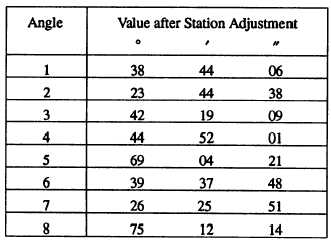
The check for average triangle closure is made after
the station adjustment. Suppose that, for the
quadrilateral shown in figure 15-28, the values of the
as follows:
15-37