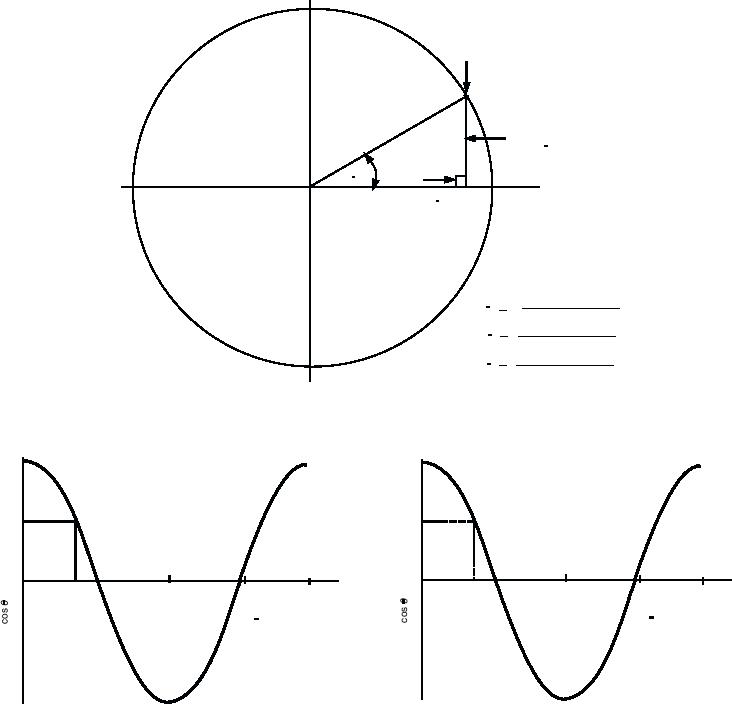
POINT
P
HYPOTENUSE
(RADIUS)
r
(SIDE
OPPOSITE 0 )
y
RIGHT
0
ANGLE
x
(SIDE ADJACENT TO 0 )
y
length of the opposite side
sin 0 = =
r
length of the hypotenuse
x
length of the adjacent side
cos 0 =
=
r
length of the hypotenuse
y
lengthof the opposite side
tan 0 =
=
x
length of the adjacent side
DCf1201
Figure 12-1. Trigonometric relationships.
1
1
0.5
0.5
0
0
o
o
o
o
270
180 o
o
360
o
o
270
60
180 o
360
o
60
90
90
0 (DEGREES)
0 (DEGREES)
-1
-1
DCf1203
DCf1203
Figure 12-3. Cosine curve.
Figure 12-2. Sine curve.
Tangent
Cosine
The tangent of the angle θ is the ratio of the side
The cosine is the ratio expressed by dividing the
side adjacent to the angle θ by the hypotenuse.
opposite the angle θ to the side adjacent. Again,
Therefore, referring to figure 12-1:
referring to figure 12-1:
cos θ = x divided by r (the adjacent divided by
Tan θ = y divided by x (the side opposite θ
the hypotenuse)
divided by the side adjacent θ)
In contrast to the sine, the cosine decreases as the
angle θ becomes larger. This relationship between the
PRINCIPLES OF PHYSICS
value of the cosine and the size of the angle is shown by
There are certain principles of physics that you
the cosine curve shown in figure 12-3. At 0 the cosine
n e e d t o k n ow i n o r d e r t o h ave a n a d e q u a t e
equals one; at 90 the cosine equals zero; and at 60 the
cosine is half the value of the cosine at 0.
understanding of stability. You should be familiar with
12-2

