It is obvious that displacement will vary with the
depth of a ship's keel below the water line that is known
as draft. As the draft increases, the displacement
increases. This is indicated in figure 12-13 by a series
1'
of displacements shown for successive draft lines on
1'
1'
the midship section of a ship. The volume of an
6'
underwater body for a given draft line can be measured
1'
in the drafting room by using graphic or mathematical
means. This is done for a series of drafts throughout the
6'
probable range of displacements in which a ship is
DCf1212
likely to operate. The values obtained are plotted on a
grid on which feet of draft are measured vertically and
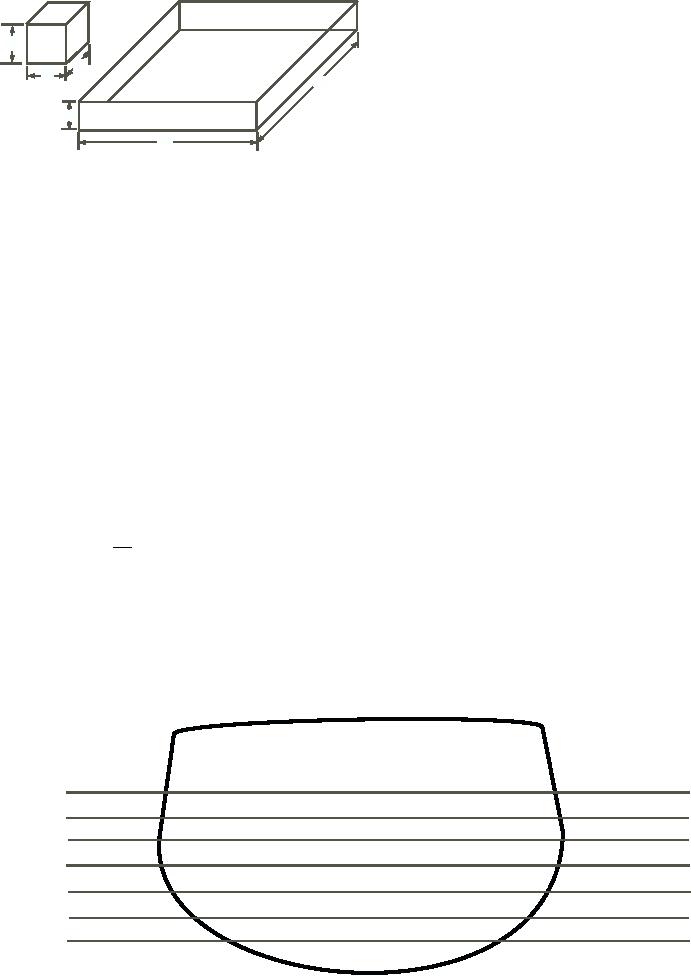
Figure 12-12. A steel cube, and a box made from the same
tons of displacement horizontally. A smooth line is
volume of steel.
faired through the points plotted, providing a curve of
displacement versus draft, or a DISPLACEMENT
It is obvious, then, that the volume of the submerged
CURVE as it is generally called. An example of this for
part of a floating ship provides the buoyancy to keep the
a typical warship is shown in figure 12-14.
ship afloat. If the ship is at rest, the buoyancy (which is
To use the sample curve shown in figure 12-14 for
the weight of the displaced water) must be equal to the
finding the displacement when the draft is given, locate
weight of the ship. For this reason, the weight of a ship is
the value of the mean draft on the draft scale at the left.
generally referred to as DISPLACEMENT, meaning the
Then proceed horizontally across the diagram to the
weight of the volume of water displaced by the hull.
displacement curve. From this point proceed vertically
Since weight (W) is equal to the displacement, it is
downward and read the displacement from the scale.
possible to measure the volume of the underwater body
For example, if you have a mean draft of 26 feet, the
(V) in cubic feet and multiply this volume by the
displacement found from the curve is approximately
weight of a cubic foot of seawater to determine what
16,300 tons.
the ship weighs. This relationship may be written as the
following:
Reserve Buoyancy
1
The volume of the watertight portion of the ship
(1) W = V
above the waterline is known as the ship's reserve
35
bu oy a n cy. E x p r e s s e d a s a p e r c e n t a g e , r e s e r ve
(2) V = 35W
buoyancy is the ratio of the volume of the above-water
body to the volume of the underwater body. Thus
V = Volume of displaced seawater (in cubic feet)
reserve buoyancy may be stated as a volume in cubic
W = Weight in tons
feet, as a ratio or percentage, or as an equivalent weight
35 = Cubic feet of seawater per ton (For ships, the
of seawater in tons. (In tons it is 1/35 of the volume in
long ton of 2,240 pounds is used.)
cubic feet of the above-water body.)
DISPLACEMENT
WATERLINE
18,000 TONS
28 FEET
14,800 TONS
24 FEET
20 FEET
11,750 TONS
8,800 TONS
16 FEET
5,900 TONS
12 FEET
DCf1213
Figure 12-13. Example of displacement data.
12-6

