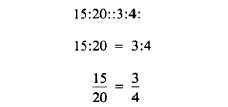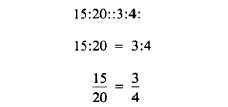Reciprocal is also used in problems involving
trigonometric functions of angles, as you will see
later in this chapter, in the solutions of problems
containing identities.
is formed. The proportion may be written in three
different ways, as in the following examples:
RATIO AND PROPORTION
Almost every computation you will make as
an EA that involves determining an unknown
value from given or measured values will involve
the solution of a proportional equation. A
thorough understanding of ratio and proportion
will greatly help you in the solution of both
surveying and drafting problems.
The results of observation or measurement
often must be compared to some standard value
in order to have any meaning. For example, if the
magnifying power of your telescope is 20
diameters and you see a telescope in the market
that says 50 diameter magnifying power, then one
can see that the latter has a greater magnifying
power. How much more powerful? To find out,
we will divide the second by the first number,
which is
The magnifying power of the second telescope is
2 1/2 times as powerful as the first. When the
relationship between two numbers is shown this
way, the numbers are compared as a RATIO. In
mathematics, a ratio is a comparison of two
quantities. Comparison by means of a ratio is
limited to quantities of the same kind, For
example, in order to express the ratio between
12 ft and 3 yd, both quantities must be written
in terms of the same unit. Thus, the proper
form of this ratio is 4 yd:3 yd, not 12 ft:3 yd.
When the parts of the ratio are expressed in
terms of the same unit, the units cancel each
other and the ratio consists simply of two
numbers. In this example, the final form of the
ratio is 4:3.
Since a ratio is also a fraction, all the rules
that govern fractions may be used in working with
ratios. Thus, the terms may be reduced, increased,
simplified, and so forth, according to the rules
for fractions.
Closely allied with the study of ratio is the
subject of proportion. A PROPORTION is
nothing more than an equation in which the
members are ratios. In other words, when two
ratios are set equal to each other, a proportion
The last two forms are the most common. All of
these forms are read, “15 is to 20 as 3 is to 4.”
In other words, 15 has the same ratio to 20 as 3
has to 4.
The whole of chapter 13, NAVEDTRA
10069-D1, is devoted to an explanation of ratio
and proportion, the solution of proportional
equations, and the closely related subject of
variation. In addition to gaining this knowledge,
you should develop the ability to recognize a
computational situation as one that is available
to solution by proportional equation. A very large
area of surveying computations—the area that
involves triangle solutions—uses the proportional
equation as the principal key to the determination
of unknown values on the basis of known values.
Practically any problem involving the conversion
of measurement expressed in one unit to the
equivalent in a different unit is solvable by
proportional equation. Similarly, if you know the
quantity of a certain material required to produce
a certain number of units of product, you can
determine by proportional equation the quantity
required to produce any given number of units.
In short, it is difficult to imagine any
mathematical computation involving the
determination of unknown values on the basis of
known values that is not available to solution by
proportional equation.
Your knowledge of equations need not extend
beyond that required to solve linear equations;
that is, equations in which the unknown appears
with no exponent higher than 1. The equation
for example, is a linear equation, because the
unknown (technically known as the “variable’ ‘),
x, appears to only the first power. The equation
X2 + 2x = – 1, however, is a quadratic, not a
linear, equation because the variable appears to
the second power.
The whole of chapter 11 of NAVEDTRA
10069-D1 is devoted to an explanation of linear
1-7