Figure 7-11.—Graphic solution of a closed traverse by latitude
and departure.
Figure 7-11 is a graphic demonstration of the fact
that, in a closed traverse, the algebraic sum of the plus
and minus latitudes is zero; and the algebraic sum of the
plus and minus departures is zero. The plus latitude of
CA is equal in length to the sum of the two minus
latitudes of AB and BC; the minus departure of BC is
equal in length to the sum of the two plus departures of
CA and AB.
LINEAR ERROR OF CLOSURE.— In practice,
as you will learn, the sum of the north latitudes usually
differs from the sum of the south latitudes. The
difference is called the error of closure in latitude.
Similarly, the sum of the east departures usually differs
from the sum of the west departures. The difference is
called error of closure in departure.
From the error of closure in latitude and the error of
closure in departure, you can determine the linear error
of closure. This is the horizontal linear distance between
the location of the end of the last traverse line (as
computed from the measured angles and distances) and
the actual point of beginning of the closed traverse.
For example, you come up with an error of closure
in latitude of 5.23 feet and an error of closure in
departure of 3.18 feet. These two linear intervals form
the sides of a right triangle. The length of the hypotenuse
of this triangle constitutes the linear error of closure in
the traverse. By the Pythagorean theorem, the length of
the hypotenuse equals approximately 6.12 feet. Suppose
the total length of the traverse was 12,000.00 feet. Then
your ratio of linear error of closure would be
6.12:12,000.00, which approximately equates to
1:2,000.
CLOSING A TRAVERSE.— You close or balance
a traverse by distributing the linear error of closure (one
within the allowable maximum, of course) over the
traverse. There are several methods of doing this, but
the one most generally applied is based on the so-called
compass rule. By this rule you adjust the latitude and
departure of each traverse line as follows:
1. Correction in latitude equals the linear error of
closure in latitude times the length of the traverse line
divided by the total length of traverse.
2. Correction in departure equals the linear error of
closure in departure times the length of the traverse line
divided by the total length of traverse.
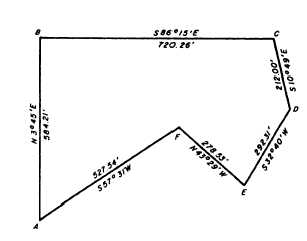
Figure 7-12 shows a closed traverse with bearings
and distances notes. Figure 7-13 shows the computation
of the latitudes and departures for this traverse entered
on the type of form that is commonly used for this
purpose. As you can see, the error in latitude is +0.33
foot, and the error in departure is +2.24 feet. The linear
error of closure, then, is
The total length of the traverse is 2614.85 feet; therefore,
the ratio of error of closure is 2.26:2614.85, or about
1:1157.
We will assume that this ratio is within the allowable
maximum. Proceed now to adjust the latitudes and
departures by the compass rule. Set down the latitudes
and departures on a form like the one shown in figure
7-14 with the error of closure in latitude at the foot of
the latitudes column and the error of closure in departure
at the foot of the departures column.
Figure 7-12.—Closed traverse by bearings and distances.
7-10