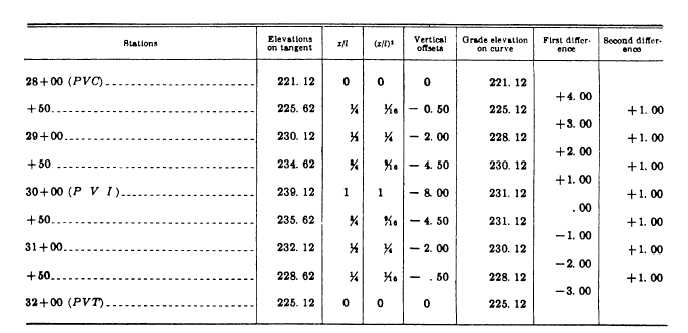
STEP 1: Prepare a table as shown in figure 11-18.
In this figure, column 1 shows the stations; column 2,
the elevations on tangent; column 3, the ratio of x/l;
column 4, the ratio of (M)*; column 5, the vertical
offsets [(x/l)*(e)]; column 6, the grade elevations on
the curve; column 7, the first difference; and column
8, the second difference.
STEP 2: Compute the elevations and set the
stations on the PVC and the PVT.
Knowing both the gradients at the PVC and PVT
and the elevation and station at the PVI, you can
compute the elevations and set the stations on the PVC
and the PVT. The gradient (g1) of the tangent at the
PVC is given as +9 percent. This means a rise in
elevation of 9 feet for every 100 feet of horizontal
distance. Since L is 400.00 feet and the curve is
symmetrical, l1 equals l2 equals 200.00 feet; therefore,
there will be a difference of 9 x 2, or 18, feet between
the elevation at the PVI and the elevation at the PVC.
The elevation at the PVI in this problem is given as
239.12 feet; therefore, the elevation at the PVC is
239.12 – 18 = 221.12 feet.
Calculate the elevation at the PVT in a similar
manner. The gradient (g2) of the tangent at the PVT is
given as –7 percent. This means a drop in elevation of
7 feet for every 100 feet of horizontal distance. Since
l1 equals l2 equals 200 feet, there will be a difference
of 7 x 2, or 14, feet between the elevation at the PVI
and the elevation at the PVT. The elevation at the PVI
therefore is
239.12 – 14 = 225,12 feet.
In setting stations on a vertical curve, remember
that the length of the curve (L) is always measured as
a horizontal distance. The half-length of the curve is
the horizontal distance from the PVI to the PVC. In
this problem, l1 equals 200 feet. That is equivalent to
two 100-foot stations and may be expressed as 2 + 00.
Thus the station at the PVC is
30 + 00 minus 2 + 00, or 28 + 00.
The station at the PVT is
30 + 00 plus 2 + 00, or 32 + 00.
List the stations under column 1.
STEP 3: Calculate the elevations at each 50-foot
station on the tangent.
From Step 2, you know there is a 9-foot rise in
elevation for every 100 feet of horizontal distance
from the PVC to the PVI. Thus, for every 50 feet of
horizontal distance, there will be a rise of 4.50 feet
in elevation. The elevation on the tangent at station
28 + 50 is
221.12 + 4.50 = 225.62 feet.
The elevation on the tangent at station 29 + 00 is
225.62 + 4.50 = 230.12 feet.
Figure 11-18.—Table of computations of elevations on a symmetrical vertical curve.
11-16