parabola is used primarily because its shape provides
a transition and, also, lends itself to the computational
methods described in the next section of this chapter.
Designing a vertical curve consists principally of
deciding on the proper length of the curve. As
indicated in figure 11-13, the length of a vertical curve
is the horizontal distance from the beginning to the
end of the curve; the length of the curve is NOT the
distance along the parabola itself. The longer a curve
is, the more gradual the transition will be from one
grade to the next; the shorter the curve, the more
abrupt the change. The change must be gradual
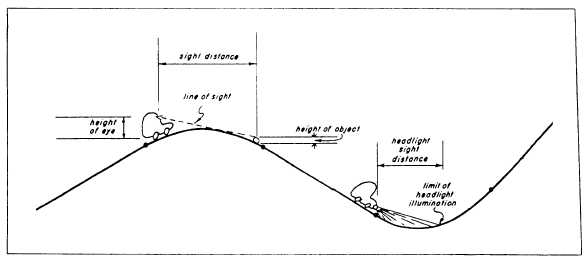
enough to provide the required sight distance (fig.
11- 14). The sight distance requirement will depend on
the speed for which the road is designed; whether
passing or nonpassing distance is required; and other
assumptions, such as one’s reaction time, braking
time, stopping distance, height of one’s eyes, and
height of objects. A typical eye level used for designs
is 4.5 feet or, more recently, 3.75 feet; typical object
heights are 4 inches to 1.5 feet. For a sag curve, the
sight distance will usually not be significant during
daylight; but the nighttime sight distance must be
considered when the reach of headlights may be
limited by the abruptness of the curve.
ELEMENTS OF VERTICAL CURVES
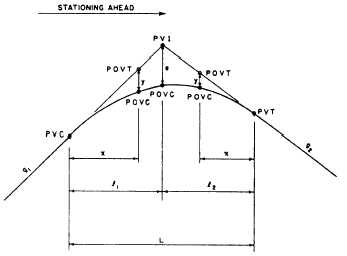
Figure 11-15 shows the elements of a vertical
curve. The meaning of the symbols and the units of
measurement usually assigned to them follow:
PVC
Point of vertical curvature; the place where the
curve begins.
PVI
PVT
POVC
POVT
gI
g2
Figure 11-15.—Elements of a vertical curve.
Point of vertical intersection; where the grade
tangents intersect.
Point of vertical tangency; where the curve
ends.
Point on vertical curve; applies to any point on
the parabola.
Point on vertical tangent; applies to any point
on either tangent.
Grade of the tangent on which the PVC is
located; measured in percent of slope.
Grade of the tangent on which the PVT is
located; measured in percent of slope.
Figure 11-14.—Sight distance.
11-13