the remainder of the stations in the same way as youwould if the transit was set over the PC. If the setupin the curve has been made but the next stake cannotbe set because of obstructions, the curve can be backedin. To back in a curve, occupy the PT. Sight on the PIand set one half of the I angle of the plates. The transitis now oriented so that, if the PC is observed, the plateswill read zero, which is the deflection angle shown inthe notes for that station. The curve stakes can then beset in the same order shown in the notes or in thereverse order. Remember to use the deflection anglesand chords from the top of the column or from thebottom of the column. Although the back-in methodhas been set up as a way to avoid obstructions, it isalso very widely used as a method for laying outcurves. The method is to proceed to the approximatemidpoint of the curve by laying out the deflectionangles and chords from the PC and then laying out theremainder of the curve from the PT. If this method isused, any error in the curve is in the center where it isless noticeable.So far in our discussions, we have begun stakingout curves by setting up the transit at the PI. But whatdo you do if the PI is inaccessible? This condition isillustrated in figure 11-11. In this situation, you locatethe curve elements using the following steps:1. As shown in figure 11-11, mark two intervisiblepoints A and B on the tangents so that line AB clears theobstacle.2. Measure angles a and b by setting up at both Aand B.3. Measure the distance AB.4. Compute inaccessible distance AV and BV usingthe formulas given in figure 11-11.5. Determine the tangent distance from the PI tothe PC on the basis of the degree of curve or other givenlimiting factor.6. 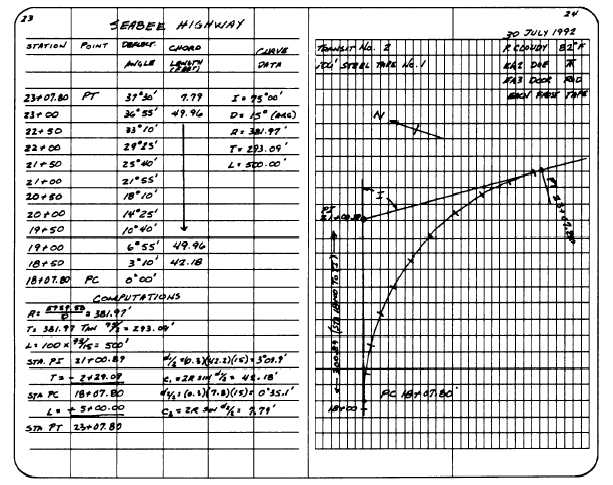Locate the PC at a distance T minus AV from thepoint A and the PT at a distance T minus BV from pointB.Field NotesFigure 11-12 shows field notes for the curve wesolved and staked out above. By now you should beFigure 11-12.—Field notes for laying out a simple curve.11-11
Integrated Publishing, Inc. - A (SDVOSB) Service Disabled Veteran Owned Small Business
