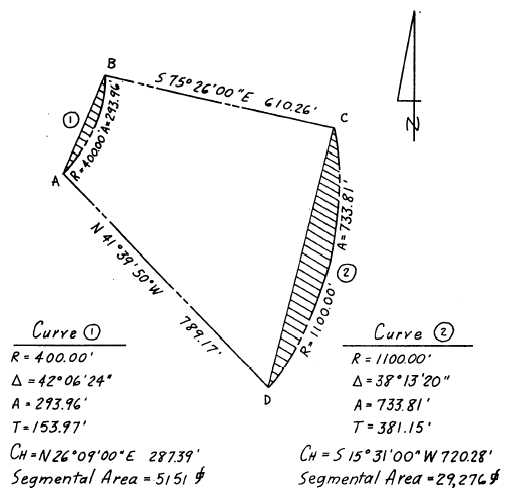
Figure 7-31.—Area within straight-line and curved-line boundaries (curved segments).
tenths; the drum, in hundredths; and the vernier, in
thousandths.
Specific instructions for using the polar planimeter
are found in the instruction booklet that is provided with
the instrument. With minimal practice, you will find that
the planimeter is a simple instrument to operate. You
should remember, though, that the accuracy obtained
with the planimeter depends mostly on the skill of the
operator in accurately tracing the boundary lines of the
figure with the tracing point of the planimeter.
If the instruction booklet has been lost, do not worry.
The planimeter can still be used. Simply determine how
many revolutions of the roller it takes to trace a figure
of known area (drawn to the same scale as the figure you
wish to determine the area of). Then trace the figure you
are working with and read the number of revolutions
taken to trace the unknown area. You now know three
values as follows: (1) the area of the figure of known
size, (2) the number of revolutions taken to trace the
figure of known size, and (3) the number of revolutions
taken to trace the figure of unknown size. B y ratio and
proportion, you can then determine the unknown area.
PARCELS THAT INCLUDE CURVES.— Not all
parcels of land are bounded entirely by straight lines.
You may have to compute the area of a construction site
that is bounded in part by the center lines or edges of
curved roads or the right-of-way lines of curved roads.
Figure 7-31 shows a construction site with a shape
similar to the traverse you have been studying in
previous examples. In this site, however, the traverse
lines AB and CD are the chords of circular curves, and
the boundary lines AB and CD are the arcs intercepted
by the chords. The following sections explain the
method of determining the area lying within the
straight-line and curved-line boundaries.
The data for each of the curves is inscribed on figure
7-31; that is, the radius R, the central angle A, the arc
length A (to be discussed in chapter 11 of this
7-21