and an engineer’s scale, just to have a general idea of
where to start. Make sure that the figure will fit
proportionately on the paper of the desired size. Starting
at point A, you draw the meridian line lightly. Then you
lay off AO, 10 inches (or any convenient round-figure
length) along the referenced meridian. Now, from O you
draw a line OP perpendicular to AO. Draw a light line
OP as shown. In a trigonometric table, look for the
natural tangent of the bearing angle 26°90', which
equals to 0.49098. Find the distance OP as follows:
OP = AO tan 26°09' = 4.9098, or 4.91 inches.
You know that OP is equal to 4.91 inches. Draw AP
extended; then you lay off the distance AB to scale along
AP. Remember that unless you are plotting a closed
traverse, it is always advantageous to start your offsets
from the referenced meridian. The reason is that, after
you have plotted three or more lines, you can always use
this referenced meridian line for checking the bearing
of the last line plotted to find any discrepancy. The
bearing angle, used as a check should also be found by
the same method (tangent-offset method).
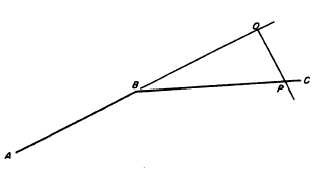
Now to plot the directions of lines from deflection
angles larger than 45°, you have to use the com-
plementary angle (90° minus the deflection angle). To
plot the direction of line BC in figure 7-37, draw a light
perpendicular line towards the right from point B.
Measure off again a convenient round-figured length,
say 10 inches, representing BOJ. The complement of the
deflection angle of BC is 90° – 78°25' = 11°35'.
The natural tangent value of 11°35’ is equal to
0.20497. From O1 draw OIP1 perpendicular to BOI.
Solving for OIPl, you will have
O]PX = BO] tan 11°35' = 2.0497, or 2.05 inches.
Now lay off the distance OIPA Draw a line from B
through PI extended; lay off the distance BC to scale
along this line. The remaining sides, CD and DA, are
plotted the same way. Make sure that the angles used for
your computations are the correct ones. A rough sketch
of your next line will always help to avoid major
mistakes.
When the deflection angle is less than 45°, the
procedure of plotting by tangent is as shown in figure
7-38. Here you measure off a convenient round-figure
length (say 500.00 feet) on the extension of the initial
traverse line to locate point O, and from O, draw OP
perpendicular to AO. The angle between BO and BC is,
Figure7-38.—Plotting by tangent-offset method from deflection
angle smaller than 45°.
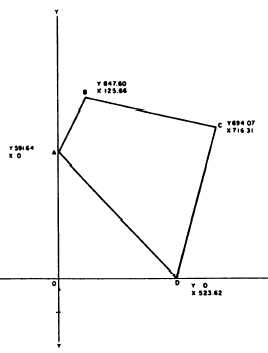
Figure 7-39.—Plotting by coordnates.
in this case, the deflection angle. Assume that
23°21'. The formula for the length of OP is
this is
OP = BO tan 23°21' = 500 x 0.43170= 215.85 feet.
PLOTTING BY COORDINATES.— A common
and accurate method of plotting by coordinates is shown
in figure 7-39. Here you simply locate each station by
its coordinates and have no angular measurements to
bother about. To plot station B, for instance, you would
layoff from O on the Y axis a distance equal to the
Y coordinate of B (847.60 feet). Draw a light line from
this point perpendicular to the Y axis, and measure off
on this line a distance equal to the X coordinate of B
(125.66 feet). The remaining points are plotted in the
same way.
7-26