3. 4. 5. 6. Measurement of angles Determination of direction (or azimuth) Base  line  measurement Computations Reconnaissance The first consideration with regard to the selection of stations is, of cause, intervisibility. An  observation between  two  stations  that  are  not  intervisible  is impossible.  Next  comes  accessibility.  Obviously  again, a station that is inaccessible cannot be occupied and between two stations otherwise equally feasible, the one that  provides  the  easier  access  is  preferable. The next consideration involves  strength of figure. In  triangulation,  the  distances  computed  (that  is,  the lengths of triangle sides) are computed by way of the law of sines. Ths more nearly equal the angles of a triangle are, the less will be the ratio of error in the sine computations. The ideal triangle, then would be one in which  each  of  the  three  angles  measured  60°;  this triangle  would,  of  course,  be  both  equiangular  and equilateral. Values  computed  from  the  sines  of  angles  near  0° or 180° are subject to large ratios of error. As a general rule,  you  should  select  stations  that  will  provide triangles in which no angle is smaller than 30° or larger than 150°. Signal Erection After   the   stations   have   been   selected,   the triangulation signals or triangulation towers should be erected  When  you  erect  triangulation  towers  or  signals, remember that it is imperative for these stations to be intervisible. It is also important that the target be large enough to be seen at a distance; that is, the color of the target  must  be  selected  for  good  visibility  against  the background  where  it  will  be  viewed.  When  observations are made during daylight hours with the sun shining, a heliotrope  is  a  very  effective  target.  When  triangulation surveys are made at night, lights must be used for targets. Therefore, target sets with built-in illuminations are very effective. Measurement  of  Angles The precision with which angles in the system are measured  will  depend  on  the  order  of  precision prescribed  for  the  survey.  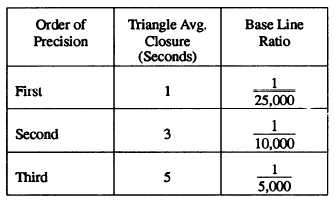The  precision  of  a triangulation system may be classified according to (1) the average error of closure of the triangles in the system and (2) the ratio of error between the measured length of a base line and its length as computed through the system  from  an  adjacent  base  line.  Large  government triangulation   surveys   are   classified   in   precision categories as follows: 15-32 For  third-order  precision,  angles  measured  with  a 1-minute  transit  will  be  measured  with  sufficient precision if they are repeated six times. As explained in chapter 13 of the EA3 TRAMAN, six repetitions with a 1-minute  transit  measures  angles  to  the  nearest  5 seconds.  To  ensure  elimination  of  certain  possible instrumental  errors,  you  should  make  half  of  the repetitions  with  the  telescope  erect  and  half  with  the telescope reversed. In each case, the horizon should be closed  around  the  station. Determination of Direction As  you  learned  earlier  in  this  chapter,  most astronomical  observations  are  made  to  determine  the true meridian from which all azimuths are referred In first-order  triangulation  systems,  these  observations  are used to determine latitude and longitude. Once the true meridian is established, the azimuths of all other sides are computed from the true meridian. To   compute   the   coordinates   of   triangulation stations,   you   must   determine   the   latitudes   and departures of the lines between stations; to do this, you must  determine  the  directions  of  these  lines.  The latitude of a traverse line means the length of the line as  projected  on  the  north-south  meridian  running through the point of origin. The departure of a traverse line means the length of the line as projected on the east-west parallel running through the point of origin Latitudes and departures are discussed in detail in chapter 7 of this TRAMAN.