Table 13-2.-Triangulation Order of Precision
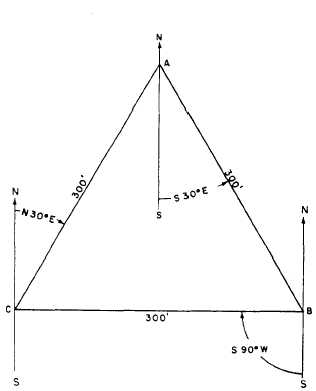
the closing traverse line, BC, shown in figure
13-27, is likely to be some distance from the
starting point, C. If this should happen, and, say,
the total accumulated linear distance measured
along the traverse lines is 900.09 ft, the ratio of
error of closure then is .09/900 or 1/10,000. This
resulting ratio is equivalent to the precision
prescribed for second order work.
Attaining Precision with a Maximum
Angular Error of Closure
You know that the sum of the interior angles
of a closed traverse should theoretically equal the
product of 180° (n – 2), n being the number of
sides in the polygon described by the traverse. A
prescribed MAXIMUM ANGULAR ERROR OF
CLOSURE is stated in terms of the product of
a given angular value times the square root of the
number of interior angles in the traverse.
Again, if we use the traverse shown in figure
13-27 as an example, the prescribed maximum
angular error of closure in minutes is 01 fi
because the figure has three interior angles. The
sum of the interior angles should be 180°. If the
Figure 13-27.-An example of a closed traverse with a perfect
sum of the angles as actually measured and
(zero-error) closure.
recorded is 179°57´, the angular error of closure
is 03´. The maximum permissible error of closure
13-23