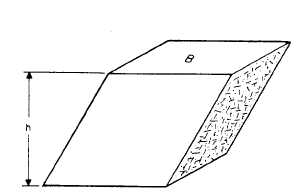
Figure 1-17.-Parts of a prism (triangular).
a solid. For example, three rectangles and
two triangles may be combined as shown in
figure 1-17. The flat surfaces of the solid figure
are its FACES, the top and bottom faces are the
BASES, and the faces forming the sides are the
LATERAL FACES or SURFACES.
Some solid figures do not have any flat faces,
and some have a combination of curved surfaces
and flat surfaces. Examples of solids with
curved surfaces include cylinders, cones, and
spheres. Those solids having no flat faces include
a great majority of natural objects, such as rocks,
living matter, and many other objects that have
irregular surfaces.
A solid figure whose bases or ends are similar,
equal, and parallel polygons, and whose faces are
parallelograms, is known geometrically as a
PRISM. The name of a prism depends upon its
base polygons. If the bases are triangles, as in
figure 1-17, the figure is a TRIANGULAR
PRISM. A RECTANGULAR PRISM has bases
that are rectangles, as shown in figure 1-18. If the
bases of a prism are perpendicular to the planes
forming its lateral faces, the prism is a RIGHT
prism.
A PARALLELEPIPED is a prism with
parallelograms for bases. Since the bases are
parallel to each other, this means that they cut
the lateral faces to form parallelograms. If a
parallelepipeds is a right prism and if its bases are
rectangles, it is a rectangular solid. A CUBE
is a rectangular solid in which all of the six
rectangular faces are squares.
Figure 1-18.-Rectangular prism, showing its height when
not a right prism.
In determining the volume of most solids, you
should use the following general formula:
V = B h
Where V = the volume
B = the area of the base or end area
h = the height of the solid (the
perpendicular height from its
base)
Volume of a Prism
For the volume of any prism, then, you simply
determine the end area or the base area by the
appropriate method and multiply the end area by
the length or the base area by the height.
Volume of a Cylinder
From the standpoint of volume calculation,
the only difference between a cylinder and a prism
lies in the fact that the end or base of a cylinder
is a circle rather than a polygon. Therefore, the
volume of a cylinder is equal to its end area times
its length. But you determine its end area from
the formula rrr2, which is the formula used for
computing the area of a circular plane. Therefore,
the volume of a cylinder is rtr2L.
Volume of a Cone or Pyramid
The best way to approach the problem of
determining the volume of a cone or pyramid is
on the basis of the fundamental fact that the
volume of a cone equals one-third of the volume
of the corresponding cylinder, while the volume
1-15