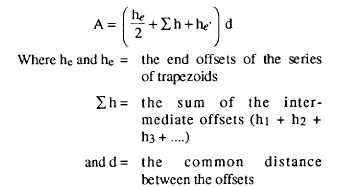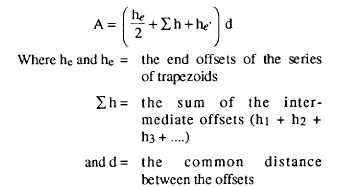Irregular Areas
Irregular areas are those areas that do not fall within
a definite standard shape. As you already have learned,
there are formulas for computing the area of a circle, a
rectangle, a triangle, and so on. However, we do not
have a standard formula for computing the area of an
irregular shaped plane, unless we use higher
mathematics (calculus), and integrate incremental areas
using lower and upper limits that define the
boundaries.
As an EA, however, most areas you will be
concerned with are those you will meet in plane
surveying. In most surveys, the computed area is the
horizontal projection of the area rather than the actual
surface of the land. The fieldwork in finding areas
consists of a series of angular and linear measurements,
defining the outline of whatever the shape is of the area
concerned, and forming a closed traverse. The
following office computation methods, which you will
learn as you advance in rate, are:
1. Plotting the closed traverse to scale and
measuring the enclosed area directly with a polar
planimeter (used only where approximate results are
required, or for checking purposes).
2. Subdividing the area into a series of triangles,
and taking the summation of all the areas of these
triangles.
3. Computing the area using the coordinates of the
individual points of the traverse (called coordinate
method).
4. Computing the area by means of the balanced
latitude and departure, and calculated DOUBLE
MERIDIAN DISTANCES of each course (called the
DMD method).
5. Computing the area by counting squares; this
method is nothing but just superimposing small squares
plotted on a transparent paper having the same scale as
the plotted traverse (or of known graphical ratio) and
counting the number of squares within the traverse. The
smaller the squares, the closer to the approximate area
you will get.
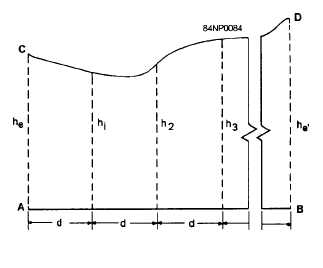
6. Computing an irregular area bounded by a curve
and perpendicular lines, as shown in figure 1-16. Here,
you can use the TRAPEZOIDAL RULE. The figure is
considered as being made up of a series of trapezoids,
all of them having the same base and having common
Figure 1-16.-Irregular area by trapezoidal rule.
distances between offsets. The formula in computing
the total area is as follows:
For the present time, try to find the areas of irregular
figures by subdividing the area to series of triangles and
by the method of counting the squares.
There are also areas of spherical surfaces and areas
of portions of a sphere. For other figures not covered
in this training manual, consult any text on plane and
solid geometry.
DETERMINING VOLUMES
From the preceding section you learned the
formulas for computing the areas of various plane
figures. These plane areas are important in the
computation of VOLUMES, as you will see later in this
section.
When plane figures are combined to form a
three-dimensional object, the resulting figure is
1-14