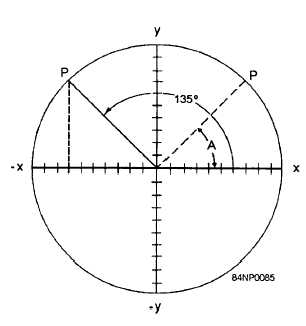
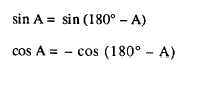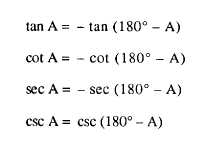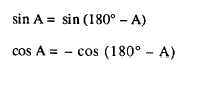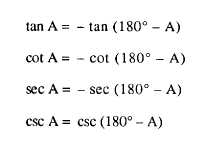Figure 1-22.-Function of an obtuse angle.
can see that the values of x, y, and r are the same for
135° as they are for 45°, except that the value of x is
negative. From this it follows that the functions of any
obtuse angle are the same as the functions of its
supplement, except that any function in which x appears
has the opposite sign.
The sine of an angle is y/r. Since x does not appear
in this function, it follows that sin A = sin (180° – A).
The cosine of an angle is fir. Since x appears in this
function, it follows that cos A = - cos (180° – A).
The tangent of an angle is y/x. Since x appears in
this function, it follows that tan A = – tan ( 180°- A).
The importance of knowing this lies in the fact that
many tables of trigonometric functions list the functions
only for angles to a maximum of 90°. Many oblique
triangles, however, contain angles larger than 90°. To
determine a function of an angle larger than 90° from a
table that stops at 90°, you lookup the function of the
supplement of the angle. If the function is a sine, you
use it as is. If it is a cosine or tangent, you give it a
negative sign.
The relationships of the function of obtuse angles
are as follows:
The above relationships apply only when angle A
is greater than 90° and less than 180°.
FUNCTIONS OF ANGLES IN
A RIGHT TRIANGLE
For an acute angle in a right triangle, the length of
the side opposite the angle corresponds to y and the
length of the side adjacent to the angle corresponds to
x, while the length of the hypotenuse corresponds to r.
Therefore, the functions of an acute angle in a right
triangle can be stated as follows:
If you consider a 90° angle with respect to the
“circle of unit radius” diagram, you will realize that for
a 90° angle, x = 0, y = 1, and r (as always) equals 1.
Since sine = y/r, it follows that the sine of 90° = 1. Since
cosine = X/r, it follows that the cosine of 90° = 0/1, or
0. Since tangent= y/x, it follows that tan 90° = 1/0, or
infinity (00). From one standpoint, division by 0 is a
mathematical inpossibility, since it is impossible to
state how many zeros there are in anything. From this
standpoint, tan 90° is simply impossible. From another
standpoint it can be said that there arc an “infinite”
number of zeros in 1. From that standpoint, tan 90° can
be said to be infinity.
In real life, the sides of a right triangle y, x, and r,
or side opposite, side adjacent, and hypotenuse, are
given other names according to the circumferences. In
connection with a pitched roof rafter, for instance, y or
side opposite is “total rise,” x or side adjacent is “total
run,” and r or hypotenuse is “rafter length.” In
connection with a ground slope, y or side opposite is
“vertical rise,” x or side adjacent is “horizontal
distance,” and r or hypotenuse is “slope distance.”
1-19