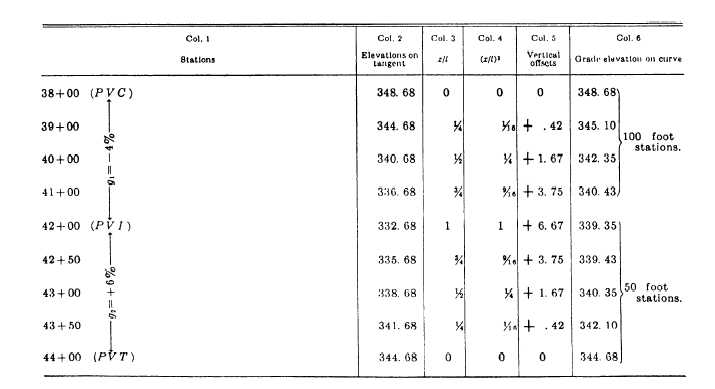
Figure 11-20.—Table of computations of elevations on an unsymmetrical vertical curve.
In this example, then, the middle vertical offset at the
PVI is calculated in the following manner:
e = [(4 x 2)/2(4 + 2)] x [(+6) - (–4)] = 6.67 feet.
Second, you are cautioned that the check on your
computations by the use of second difference does
NOT work out the same way for unsymmetrical curves
as for a symmetrical curve. The second difference will
not check for the differences that span the PVI. The
reason is that an unsymmetrical curve is really two
parabolas, one on each side of the PVI, having a
common POVC opposite the PVI; however, the
second difference will check out back, and ahead, of
the first station on each side of the PVI.
Third, the turning point is not necessarily above
or below the tangent with the lesser slope. The
horizontal location is found by the use of one of two
formulas as follows:
from the PVC
or from the PVT
The procedure is to estimate on which side of the PVI
the turning point is located and then use the proper
formula to find its location. If the formula indicates that
the turning point is on the opposite side of the PVI, you
must use the other formula to determine the correct
location; for example, you estimate that the turning
point is between the PVC and PVI for the curve in figure
11-19. Solving the formula:
xt= (l1)2(g1)/2e
xt= [(4)2(4)]/(2 x 6.67) = 4.80, or Station 42 + 80.
However, Station 42 + 80 is between the PVI and PVT;
therefore, use the formula:
xt= (l2)2(g2)//2e
xt= [(2)2(6)]/(2 x 6.67) = 1.80, or station 42 + 20.
Station 42 + 20 is the correct location of the turning
point. The elevation of the POVT, the amount of the
offset, and the elevation on the curve is determined as
previously explained.
CHECKING THE COMPUTATION
BY PLOTTING
Always check your work by plotting the grade
tangents and the curve in profile on an exaggerated
11-19