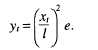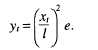For the curve we are calculating, the computations
would be (7 x 4)/16 = 1.75 feet; therefore, the turning
point is 1.75 stations, or 175 feet, from the PVT (station
30 + 25).
The vertical offset for the turning point is found
by the formula:
For this curve, then, the computation is ( 1.75/2)2 x 8 =
6.12 feet.
The elevation of the POVT at 30 + 25 would be 237.37,
calculated as explained earlier. The elevation on the
curve would be
is different from the horizontal distance between the
PVI and the PVT. In other words, l1 does NOT equal
l2. Unsymmetrical curves are sometimes described as
having unequal tangents and are referred to as dog
legs. Figure 11-19 shows an unsymmetrical curve with
a horizontal distance of 400 feet on the left and a
horizontal distance of 200 feet on the right of the PVI.
The gradient of the tangent at the PVC is –4 percent;
the gradient of the tangent at the PVT is +6 percent.
Note that the curve is in a dip.
As an example, let’s assume you are given the
following values:
Elevation at the PVI is 332.68
Station at the PVI is 42 + 00
237.37-6.12 = 231.25.
l1 is 400 feet
STEP 8: Check your work.
One of the characteristics of a symmetrical para-
bolic curve is that the second differences between
successive grade elevations at full stations are con-
stant. In computing the first and second differences
(columns 7 and 8), you must consider the plus or
minus signs. When you round off your grade elevation
figures following the degree of precision required, you
introduce an error that will cause the second difference
to vary slightly from the first difference; however, the
slight variation does not detract from the value of the
second difference as a check on your computations.
You are cautioned that the second difference will not
always come out exactly even and equal. It is merely
a coincidence that the second difference has come out
exactly the same in this particular problem.
Unsymmetrical Vertical Curves
An unsymmetrical vertical curve is a curve in
which the horizontal distance from the PVI to the PVC
l2 is 200 feet
g1 is –4%
g2 is +6%
To calculate the grade elevations on the curve to the
nearest hundredth foot, use figure 11-20 as an example.
Figure 11-20 shows the computations. Set four
100-foot stations on the left side of the PVI (between
the PVI and the PVC). Set four 50-foot stations on the
right side of the PVl (between the PVI and the PVT).
The procedure for solving an unsymmetrical curve
problem is essentially the same as that used in solving
a symmetrical curve. There are, however, important
differences you should be cautioned about.
First, you use a different formula for the
calculation of the middle vertical offset at the PVI. For
an unsymmetrical curve, the formula is as follows:
Figure 11-19.—Unsymmetrical vertical curve.
11-18