AREA BY DOUBLE MERIDIAN DISTANCE.—
The meridian distance of a traverse line is equal to the
length of a line running east to west from the midpoint
of the traverse line to a reference meridian. The
reference meridian is the meridian that passes through
the most westerly traverse station.
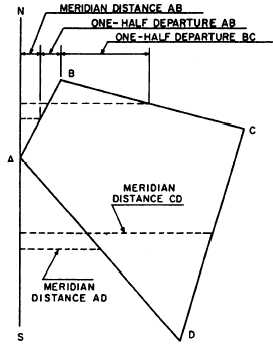
In figure 7-20, the dotted lines indicate the meridian
distances of the traverse lines to which they extend from
the reference meridians. You can see that the meridian
distance of the initial line AB equals one half of the
departure of AB. The meridian distance of the next line
BC equals the meridian distance of AB, plus one half of
the departure of AB, plus one half of the departure of
BC.
You can also see that the meridian distance of CD
equals the meridian distance of BC, plus one half of the
departure of BC, minus one half of the departure of DC.
Similarly, the meridian distance of AD equals the
meridian distance of DC, minus one half of the
departure of DC, minus one half of the departure of AD.
You should now be able to understand the basis for
the following rules for determining meridian distance:
1. For the initial traverse line in a closed traverse,
the meridian distance equals one half of the departure.
2. For each subsequent traverse line, the meridian
distance equals the meridian distance of the preceding
Figure 7-19.—Form for computing coordinates
Figure 7-20.—Meridian distances.
line, plus one half of the departure of the preceding line,
plus one half of the departure of the line itself. However,
it is the algebraic sum that results—meaning that plus
departures are added but minus departures are
subtracted.
7-15