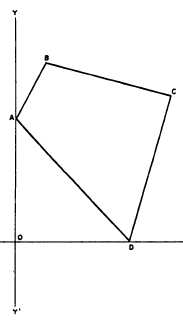
Figure 7-23.—Area from double parallel distances.
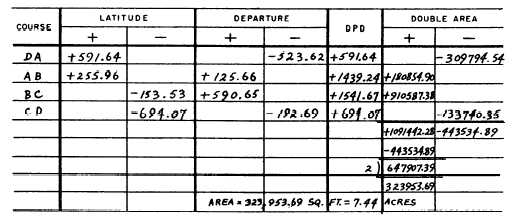
The double area of DA is
523.62 x 591.64 = 309,794.54 square feet.
The difference between the sum of the minus double
areas and the sum of the plus double areas is the double
area which is 647,907.39 square feet. The area is one
half of this, or 323,953.69 square feet. Land area is
generally expressed in acres. There are 43,560 square
feet in 1 acre; therefore, the area in acres is
AREA BY DOUBLE PARALLEL DISTANCE.—
You can check the accuracy of the area computation of
a DMD by computing the same area from double
parallel distances (DPD).
As shown in figure 7-22, the parallel distance of a
traverse line is the north-to-south distance from the
midpoint of the line to a reference parallel. The reference
parallel is the parallel passing through the most
southerly traverse station.
You can see that the solution for parallel distance is
the same as the one used for meridian distance, except
that to compute parallel distance you use latitude instead
of departure. The parallel distance of the initial traverse
line (which is DA in this case) equals one half of the
latitude. The parallel distance of the next line, AB, equals
the parallel distance of the preceding line, DA, plus one
half of the latitude of the preceding line DA, plus one
half of the latitude of line AB itself.
It follows from the above that the DPD of the initial
traverse line DA equals the latitude of the line. The DPD
of the next line, AB, equals the DPD of the preceding
line, DA, plus the latitude of the preceding line, DA, plus
the latitude of the line AB itself. The solution for area is
the same as for area by meridian distance except that,
for the double area of each traverse line, you multiply
the DPD by the departure instead of multiplying the
DMD by the latitude.
Figure 7-23 shows entries for the computation of the
area of DPD for the traverse we are working on. Note
that the result is identical with that obtained by the
computation of the DMD.
AREA FROM COORDINATES.— Before we
explain the method of computing area from coordinates,
let us set coordinates for the stations of the traverse we
are working on. To avoid using negative coordinates, we
will measure Y coordinates from an X axis passing
through the most southerly station and X coordinates
from a Y axis passing through the most westerly station,
as shown in figure 7-24.
Figure 7-24.—Computations of a closed traverse by coordinate
method.
7-17