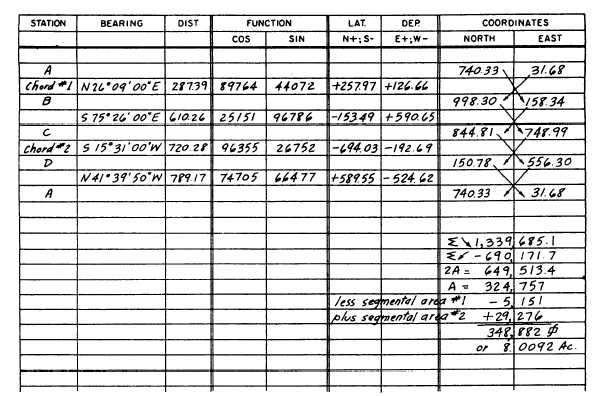
Figure 7-32.—Computation of area which includes curve segments.
TRAMAN), the tangent length T and the chord bearing
and distance C~.
The crosshatched areas lying between the chord
and arc are called segmental areas. To determine the
area of this parcel, you must (1) determine the area
lying within the straight-line and chord (also straight-
line) boundaries, (2) determine the segmental areas,
(3) subtract the segmental area for Curve 1 from the
straight-line boundary area and (4) add the segmental
area for Curve 2 to the straight-line boundary area.
The method of determining a segmental area was
explained in the EA3 TRAMAN. The straight-line area
may be determined by the coordinate method, as
explained in this chapter. For figure 7-31, the segmental
area for Curve 1 works out to be 5,151 square feet; for
Curve 2, it is 29,276 square feet.
Figure 7-32 shows atypical computation sheet for
the area problem shown in figure 7-31. Included with
the station letter designations in the station column are
designations (Chord #1 and Chord #2) showing the
bearings and distances that constitute the chords of
Curves 1 and 2. The remainder of the upper part of the
form shows the process (with which you are now
familiar) of determining latitudes and departures from
the bearings and distances, coordinates from the
latitudes and departures, double areas from cross
multiplication of coordinates, double areas from the
difference between the sums of north and sums of east
coordinates, and areas from half of the double areas. As
you can see in figure 7-32, the area within the
straight-line boundaries is 324,757 square feet. From
this area, segmental area No. 1 is subtracted. Then
segmental area No. 2 is added.
To obtain the area of the parcel as bounded by the
arcs of the curves, you must add or subtract the
segmental areas depending on whether the particular
area in question lies inside or outside of the actual
curved boundary. In figure 7-31, you can see that the
segmental area for Curve 1 lies outside and must be
subtracted from the straight-line area, while that for
Curve 2 lies inside and must be added. With the
segmental areas accounted for, the area comes to
348,882 square feet or 8.01 acres.
The second method of determining a curved-
boundary area makes use of the external areas rather
than the segmental areas of the curves, as shown in
figure 7-33. The straight-line figure is defined by the
tangents of the curves, rather than by the chords. This
method may be used as an alternative to the chord
method or to check the result obtained by the chord
method.
The computation sheet shown in figure 7-34 follows
the same pattern as the one shown in figure 7-32.
However, there are two more straight-line boundaries,
7-22