vertical distance from your eye level to the ground is 5.7
feet. ‘Then with the hand level at your eye and with you
standing on station A, the HI is
112.5 + 5.7= 118.2 feet.
If a level rod is set up anywhere on the 112.0-foot
contour, the reading you would get from station A would
be
118.2 – 112.0= 6.2 feet.
Therefore, to determine the point where the 112.0 foot
contour crosses AB, you only need to have the rodman
back out from point A along AB until he comes to the
point where you read 6.2 feet on the rod. You can
determine the point where the 112.0-foot contour
crosses AD in the same reamer as AB. You can measure
the distance from A to each point and then record the
distance from A to the 112.0-foot contour on AB and AD.
When all of the contours have been located on AB
and AD, you can shift to station C and carry out the same
procedure to locate the contours along BC and CD. You
have now located all the points where contours at a
l-foot interval intersect the traverse lines. If the slope of
the ground is uniform (as it is presumed to be in fig.
8-13), you can plot the contour lines by simply drawing
lines between points of equal elevation, as shown in that
figure. If there were irregularities in the slope, you
would send the rodman out along one or more lines laid
across the irregular ground, locating the contours on
these lines as you located them on the traverse lines.
Grid Coordinate System
In the grid coordinate system, the area is laid out in
squares of convenient size, and the elevation of each
comer point is determined. While this method lends
itself to use on relatively level ground, ridge or valley
lines must be located by spot elevations taken along the
lines. The locations of the desired contours are then
determined on the ridge and valley lines and on the sides
of the squares by interpolation. This gives a series of
points through which the contour lines may be drawn
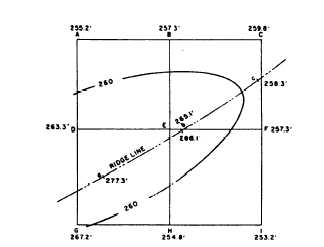
Figure 8-14 illustrates this method. Assume that the
squares here measure 200.0 feet on each side. Points a,
b, and c are points on a ridge line, also 200.0 feet apart.
You need to locate and draw the 260.0-foot contour line.
By inspection, you can see that the 260.0-foot contour
must cross AD since the elevation of A is 255.2 feet and
the elevation of D is 263.3 feet. However, at what point
does the 260.0-foot contour cross AD? This can be
determined by using a proportional equation as follows.
Figure 8-14.-Grid system of ground points
Assume that the slope from A to D is uniform. The
difference in elevation is 8.1 feet (263.3 – 255.2) for
200.0 feet. The difference in elevation between 255.2
and 260.0 feet (elevation of the desired contour) is 4.8
feet. The distance from A to the point where
the 260.0-foot contour crosses AD is the value of x
in the proportional equation: 8.1:200 = 4.8:x or
x = 118.5 feet. Lay off 118.5 feet from A on AD and
make a mark.
In the same manner, you locate and mark the points
where the 260.0-foot contour crosses BE,EF, EH, and
GH. The 260.0-foot contour crosses the ridge,
obviously, between point b (elevation 266.1 feet) and
point c (elevation 258.3 feet). The distance between b
and c is again 200.0 feet. Therefore, you obtain the
location of the point of crossing by the same procedure
just described.
You now have six plotted points: one on the ridge
line between b and c and the others on AD, BE, EF, EH,
and GH. A line sketched by hand through these points
is the 260.0-foot contour line. Note that the line is, in
effect, the line that would be formed by a horizontal
plane that passed through the ridge at an elevation of
260.0 feet. Note, too, that a contour line changes
direction at a ridge summit.
Control Points
This explanation illustrates the fact that any contour
line may be located by interpolation on a uniform slope
between two points of known elevation a known
distance apart. We, also, demonstrated how a ridge line
is located in the same manner.
If you locate and plot all the important irregularities
8-14
in an area (ridges, valleys, and any other points where