and marked point when rays from A and B will give a strong intersection (angle  ADB is greater than 300). First set up and level the plane table at point D (first setup, fig. 9-4). Using plotted points  a and b, draw resection rays from A and B. These rays  intersect at d which is the tentative position of D. Draw a ray from d’ toward C. Plot c’ on this line at the estimated distance from D to C. Next, set up the plane table at  C  (second  setup,  fig. 9-4) and orient by backlighting on D. Sight on A and draw a ray through c’ intersecting line ad’ at a’. In a like manner, sight on  B to establish  b’. You  now  have a quadrilateral a’b’d’c’  that is similar to ABDC. Since, in these similar quadrilaterals, line  a’b’ should always be  parallel  to  line  AB,  the  error  in  orientation  is indicated  by  the  angle  between  ab and a’b’. To correct the orientation, place the alidade on line a’b’ and sight on a distinctive distant point. Then move the alidade to line  ab and rotate the table to sight on  the  same  distant  point.  The  plane  table  is  now oriented, and resection lines from A and B through a and b plot  the  position  of  point  C. 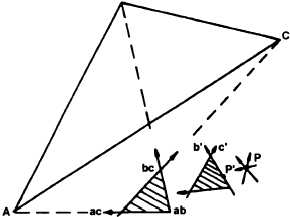THREE-POINT  METHOD.—  The  three-point method involves orienting the plane table and plotting a station when three known plotted stations can be seen  but  not  conveniently  occupied. Set up the plane table at the unknown point  P (fig. 9-5) and approximately orient the table by eye or compass. Draw rays to the known points  A, B, and C. The point ab denotes the intersection of the ray to A with the ray to B. Points bc and ac are similar in their notation. If the plane table is oriented properly, the B Figure 9-5.—Three-point method of resection. three rays will intersect at a single point. Usually, however, the first orientation is not accurate, and the rays intersect at three points  (ab, bc, and ac) forming a triangle, known as the triangle of error. From the geometry involved, the location of the desired  point,   P, must  fulfill  the  following  three conditions  with  respect  to  the  triangle: 1. It will fall to the same side of all three rays; that is, either to the right or to the left of all three rays. 2. It will be proportionately as far from each ray as the distance from the triangle to the respective plotted point. 3.  It  will  be  inside  the  triangle  of  error  if  the triangle  of  error  is  inside  of  the  main  plotted  triangle and outside the triangle of error if it is outside the main triangle. In figure 9-5, notice that the triangle of error is outside the main triangle, and almost twice as far from B as from A, and about equally as far from C as from B. The desired point,  P, must  be  about  equidistant from the rays to B, and to C, and about one half as far from the ray to A, and the three measurements must be made to the same side of the respective rays. As drawn, only one location will fulfill all these conditions and that is near P’. This is assumed as the desired location. The plane table is reoriented using P’ and back- lighting on one of the farther points  (B). The new rays (a’, b’, and c’) are drawn. Another (smaller) triangle of error results. This means that the selected position, P’, was not quite far enough. Another point,  P, is  selected using the above conditions, the table is reoriented, and the new rays are drawn. If the tri- angle had become larger, a mistake was made and the selected point was on the wrong side of one of the rays. The directions should be rechecked and the point reselected in the proper   direction. The new point, P, shows no triangle of error when the rays are drawn. It can be assumed to be the desired location of the point over which the plane table is set. In  addition,  the  orientation  is  correct.  Using  a  fourth known and plotted point as a check, a ray drawn from that point should also pass through  P. If not, an error has been made and the process must be repeated. Normally the second or third try should bring the triangle of error down to a point. If, after the third try, the triangle has not decreased to a point, you should draw a circular arc through one set of intersections  (ab, a’b’) and another arc through either of the other sets (bc, b’c’, or ac, a’c’).  The intersections of the two arcs 9-4