trapezoids. Then, by computing the area of each
triangle and trapezoid and determining the sum of the
areas, you obtain the area of the polygon.
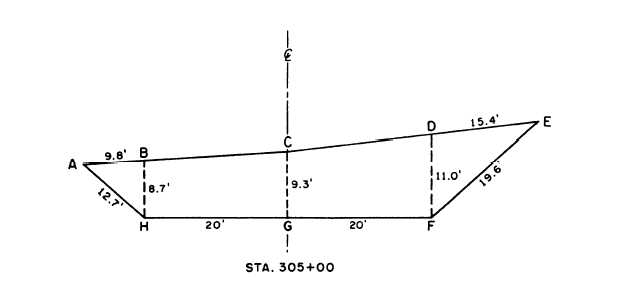
Take, for example, the plot of station 305 + 00
shown in figure 10-4. Figure 10-5 illustrates how this
figure can be resolved into two triangles, ABH and
DFE, and two trapezoids, BCGH and CGFD. For each
of these figures, the approximate dimensions have
been determined by the scale of the plot. From your
knowledge of mathematics, you know that the area of
each triangle can be determined using the following
formula:
Where:
s = one half of the perimeter of the triangle,
and that for each trapezoid, you can calculate the area
using the formula:
When the above formulas are applied and the sum
of the results are determined, you find that the total
area of the cross section at station 305 is 509.9
square feet.
AREA BY FORMULA.— A regular section area
for a three-level section can be more exactly
determined by applying the following formula:
Figure 10-4.—A cross section plotted on cross-section paper.
Figure 10-5.—Cross section resolved into triangles and trapezoids.
10-8